Stochastic Shortest Path with Energy Constraints in POMDPs

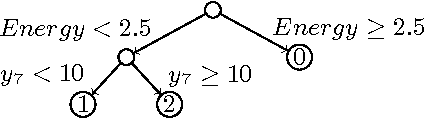
We consider partially observable Markov decision processes (POMDPs) with a set of target states and positive integer costs associated with every transition. The traditional optimization objective (stochastic shortest path) asks to minimize the expected total cost until the target set is reached. We extend the traditional framework of POMDPs to model energy consumption, which represents a hard constraint. The energy levels may increase and decrease with transitions, and the hard constraint requires that the energy level must remain positive in all steps till the target is reached. First, we present a novel algorithm for solving POMDPs with energy levels, developing on existing POMDP solvers and using RTDP as its main method. Our second contribution is related to policy representation. For larger POMDP instances the policies computed by existing solvers are too large to be understandable. We present an automated procedure based on machine learning techniques that automatically extracts important decisions of the policy allowing us to compute succinct human readable policies. Finally, we show experimentally that our algorithm performs well and computes succinct policies on a number of POMDP instances from the literature that were naturally enhanced with energy levels.

Qualitative Analysis of POMDPs with Temporal Logic Specifications for Robotics Applications

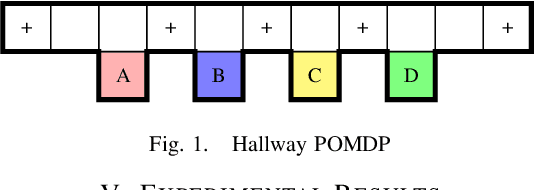
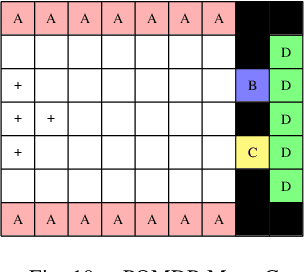
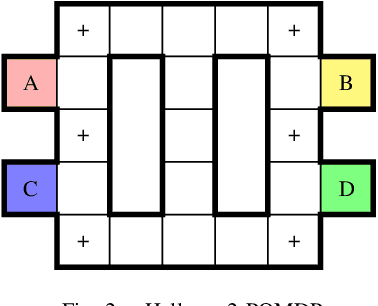
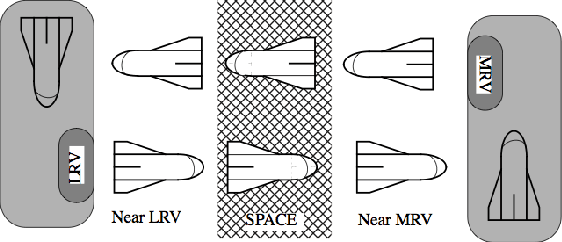
We consider partially observable Markov decision processes (POMDPs), that are a standard framework for robotics applications to model uncertainties present in the real world, with temporal logic specifications. All temporal logic specifications in linear-time temporal logic (LTL) can be expressed as parity objectives. We study the qualitative analysis problem for POMDPs with parity objectives that asks whether there is a controller (policy) to ensure that the objective holds with probability 1 (almost-surely). While the qualitative analysis of POMDPs with parity objectives is undecidable, recent results show that when restricted to finite-memory policies the problem is EXPTIME-complete. While the problem is intractable in theory, we present a practical approach to solve the qualitative analysis problem. We designed several heuristics to deal with the exponential complexity, and have used our implementation on a number of well-known POMDP examples for robotics applications. Our results provide the first practical approach to solve the qualitative analysis of robot motion planning with LTL properties in the presence of uncertainty.

Optimal Cost Almost-sure Reachability in POMDPs

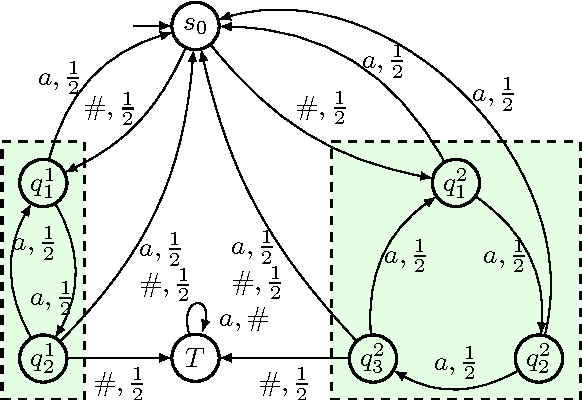
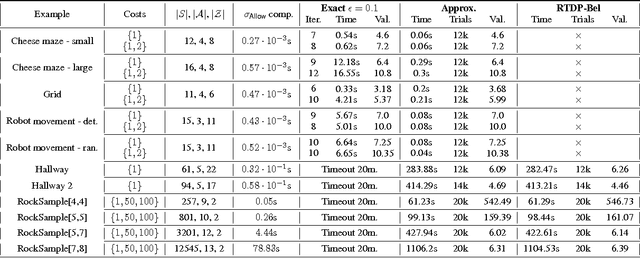
We consider partially observable Markov decision processes (POMDPs) with a set of target states and every transition is associated with an integer cost. The optimization objective we study asks to minimize the expected total cost till the target set is reached, while ensuring that the target set is reached almost-surely (with probability 1). We show that for integer costs approximating the optimal cost is undecidable. For positive costs, our results are as follows: (i) we establish matching lower and upper bounds for the optimal cost and the bound is double exponential; (ii) we show that the problem of approximating the optimal cost is decidable and present approximation algorithms developing on the existing algorithms for POMDPs with finite-horizon objectives. While the worst-case running time of our algorithm is double exponential, we also present efficient stopping criteria for the algorithm and show experimentally that it performs well in many examples of interest.

POMDPs under Probabilistic Semantics

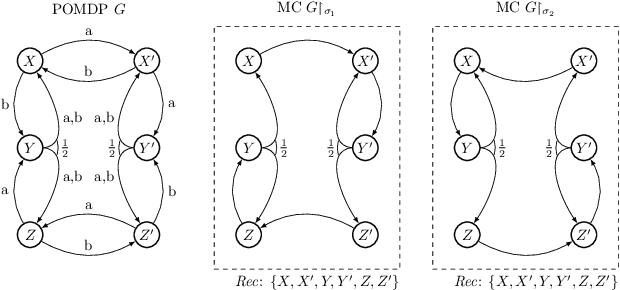
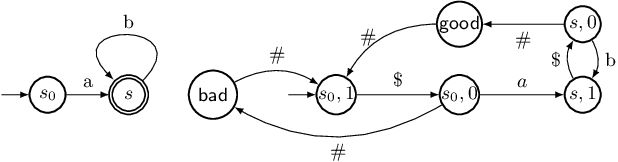
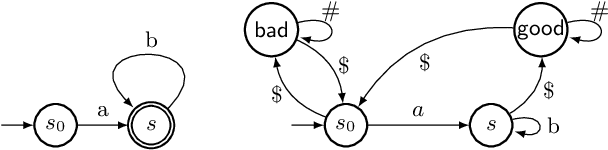
We consider partially observable Markov decision processes (POMDPs) with limit-average payoff, where a reward value in the interval [0,1] is associated to every transition, and the payoff of an infinite path is the long-run average of the rewards. We consider two types of path constraints: (i) quantitative constraint defines the set of paths where the payoff is at least a given threshold {\lambda} in (0, 1]; and (ii) qualitative constraint which is a special case of quantitative constraint with {\lambda} = 1. We consider the computation of the almost-sure winning set, where the controller needs to ensure that the path constraint is satisfied with probability 1. Our main results for qualitative path constraint are as follows: (i) the problem of deciding the existence of a finite-memory controller is EXPTIME-complete; and (ii) the problem of deciding the existence of an infinite-memory controller is undecidable. For quantitative path constraint we show that the problem of deciding the existence of a finite-memory controller is undecidable.