Learning Algorithms for Verification of Markov Decision Processes

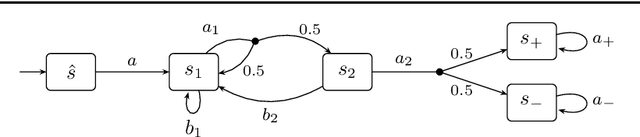
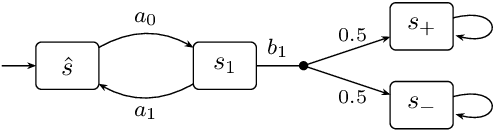
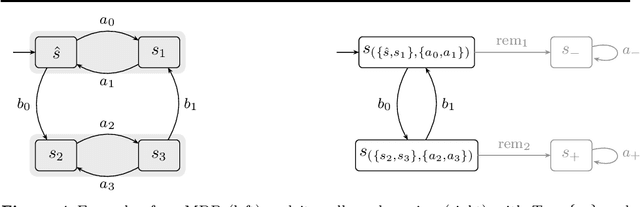
We present a general framework for applying learning algorithms and heuristical guidance to the verification of Markov decision processes (MDPs). The primary goal of our techniques is to improve performance by avoiding an exhaustive exploration of the state space, instead focussing on particularly relevant areas of the system, guided by heuristics. Our work builds on the previous results of Br{\'{a}}zdil et al., significantly extending it as well as refining several details and fixing errors. The presented framework focuses on probabilistic reachability, which is a core problem in verification, and is instantiated in two distinct scenarios. The first assumes that full knowledge of the MDP is available, in particular precise transition probabilities. It performs a heuristic-driven partial exploration of the model, yielding precise lower and upper bounds on the required probability. The second tackles the case where we may only sample the MDP without knowing the exact transition dynamics. Here, we obtain probabilistic guarantees, again in terms of both the lower and upper bounds, which provides efficient stopping criteria for the approximation. In particular, the latter is an extension of statistical model-checking (SMC) for unbounded properties in MDPs. In contrast to other related approaches, we do not restrict our attention to time-bounded (finite-horizon) or discounted properties, nor assume any particular structural properties of the MDP.

Synthesizing Efficient Solutions for Patrolling Problems in the Internet Environment

We propose an algorithm for constructing efficient patrolling strategies in the Internet environment, where the protected targets are nodes connected to the network and the patrollers are software agents capable of detecting/preventing undesirable activities on the nodes. The algorithm is based on a novel compositional principle designed for a special class of strategies, and it can quickly construct (sub)optimal solutions even if the number of targets reaches hundreds of millions.

Stochastic Shortest Path with Energy Constraints in POMDPs

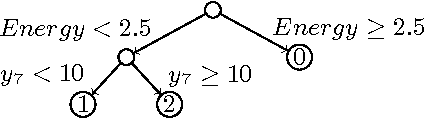
We consider partially observable Markov decision processes (POMDPs) with a set of target states and positive integer costs associated with every transition. The traditional optimization objective (stochastic shortest path) asks to minimize the expected total cost until the target set is reached. We extend the traditional framework of POMDPs to model energy consumption, which represents a hard constraint. The energy levels may increase and decrease with transitions, and the hard constraint requires that the energy level must remain positive in all steps till the target is reached. First, we present a novel algorithm for solving POMDPs with energy levels, developing on existing POMDP solvers and using RTDP as its main method. Our second contribution is related to policy representation. For larger POMDP instances the policies computed by existing solvers are too large to be understandable. We present an automated procedure based on machine learning techniques that automatically extracts important decisions of the policy allowing us to compute succinct human readable policies. Finally, we show experimentally that our algorithm performs well and computes succinct policies on a number of POMDP instances from the literature that were naturally enhanced with energy levels.

MultiGain: A controller synthesis tool for MDPs with multiple mean-payoff objectives

We present MultiGain, a tool to synthesize strategies for Markov decision processes (MDPs) with multiple mean-payoff objectives. Our models are described in PRISM, and our tool uses the existing interface and simulator of PRISM. Our tool extends PRISM by adding novel algorithms for multiple mean-payoff objectives, and also provides features such as (i)~generating strategies and exploring them for simulation, and checking them with respect to other properties; and (ii)~generating an approximate Pareto curve for two mean-payoff objectives. In addition, we present a new practical algorithm for the analysis of MDPs with multiple mean-payoff objectives under memoryless strategies.