František Blahoudek
Efficient Strategy Synthesis for MDPs with Resource Constraints
May 05, 2021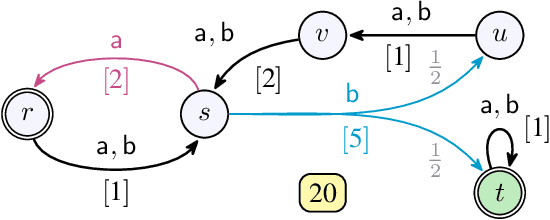
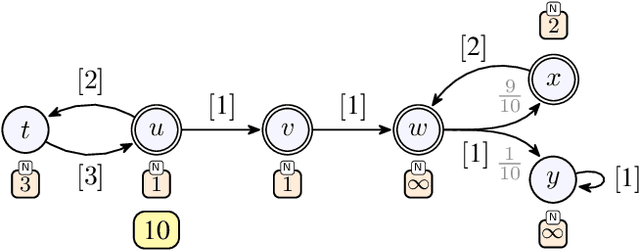
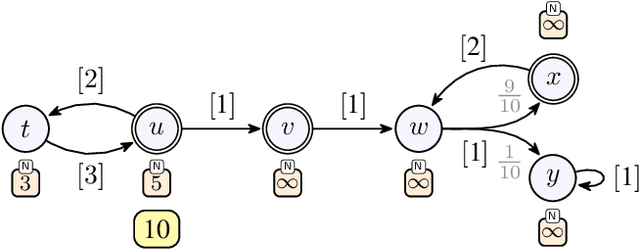
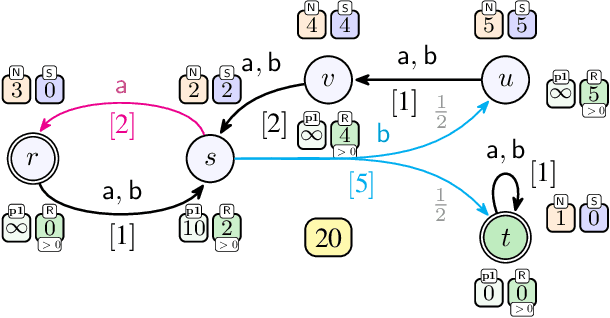
Abstract:We consider qualitative strategy synthesis for the formalism called consumption Markov decision processes. This formalism can model dynamics of an agents that operates under resource constraints in a stochastic environment. The presented algorithms work in time polynomial with respect to the representation of the model and they synthesize strategies ensuring that a given set of goal states will be reached (once or infinitely many times) with probability 1 without resource exhaustion. In particular, when the amount of resource becomes too low to safely continue in the mission, the strategy changes course of the agent towards one of a designated set of reload states where the agent replenishes the resource to full capacity; with sufficient amount of resource, the agent attempts to fulfill the mission again. We also present two heuristics that attempt to reduce expected time that the agent needs to fulfill the given mission, a parameter important in practical planning. The presented algorithms were implemented and numerical examples demonstrate (i) the effectiveness (in terms of computation time) of the planning approach based on consumption Markov decision processes and (ii) the positive impact of the two heuristics on planning in a realistic example.
Polynomial-Time Algorithms for Multi-Agent Minimal-Capacity Planning
May 04, 2021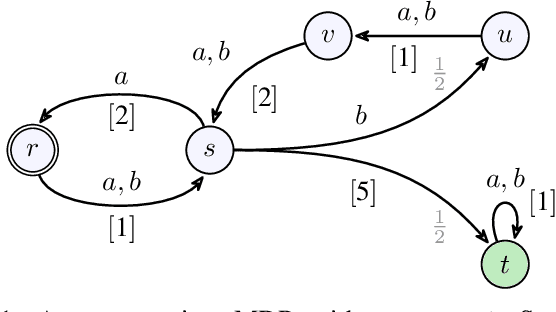
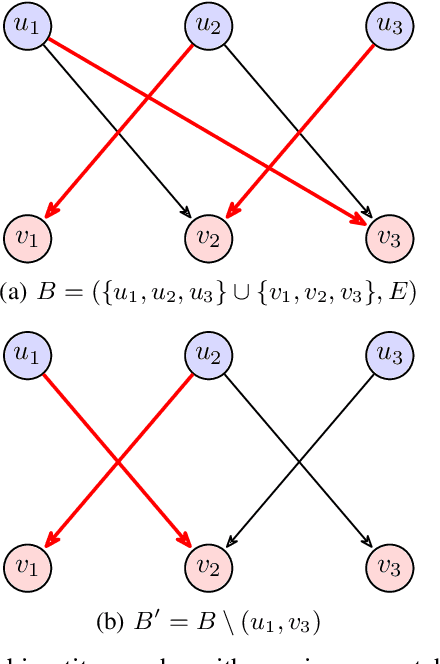
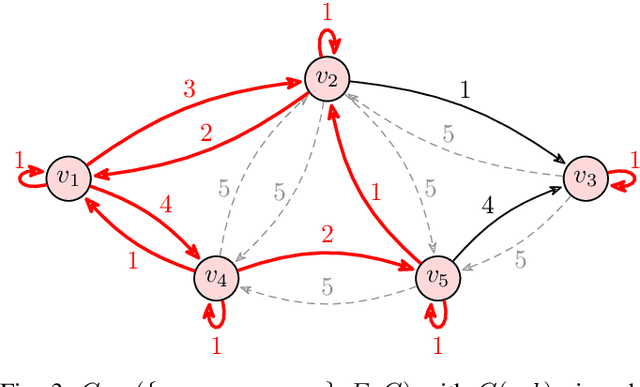
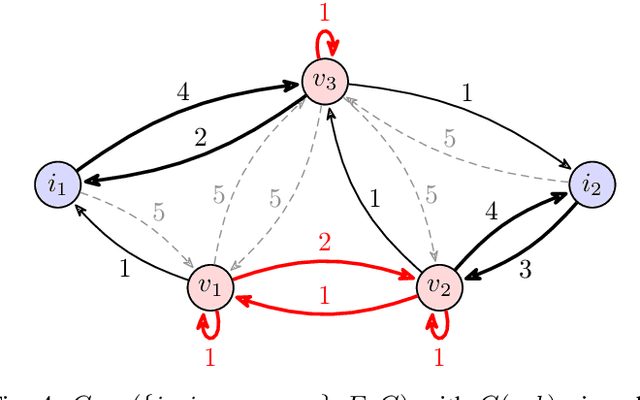
Abstract:We study the problem of minimizing the resource capacity of autonomous agents cooperating to achieve a shared task. More specifically, we consider high-level planning for a team of homogeneous agents that operate under resource constraints in stochastic environments and share a common goal: given a set of target locations, ensure that each location will be visited infinitely often by some agent almost surely. We formalize the dynamics of agents by consumption Markov decision processes. In a consumption Markov decision process, the agent has a resource of limited capacity. Each action of the agent may consume some amount of the resource. To avoid exhaustion, the agent can replenish its resource to full capacity in designated reload states. The resource capacity restricts the capabilities of the agent. The objective is to assign target locations to agents, and each agent is only responsible for visiting the assigned subset of target locations repeatedly. Moreover, the assignment must ensure that the agents can carry out their tasks with minimal resource capacity. We reduce the problem of finding target assignments for a team of agents with the lowest possible capacity to an equivalent graph-theoretical problem. We develop an algorithm that solves this graph problem in time that is \emph{polynomial} in the number of agents, target locations, and size of the consumption Markov decision process. We demonstrate the applicability and scalability of the algorithm in a scenario where hundreds of unmanned underwater vehicles monitor hundreds of locations in environments with stochastic ocean currents.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge