Qualitative Analysis of $ω$-Regular Objectives on Robust MDPs

Robust Markov Decision Processes (RMDPs) generalize classical MDPs that consider uncertainties in transition probabilities by defining a set of possible transition functions. An objective is a set of runs (or infinite trajectories) of the RMDP, and the value for an objective is the maximal probability that the agent can guarantee against the adversarial environment. We consider (a) reachability objectives, where given a target set of states, the goal is to eventually arrive at one of them; and (b) parity objectives, which are a canonical representation for $\omega$-regular objectives. The qualitative analysis problem asks whether the objective can be ensured with probability 1. In this work, we study the qualitative problem for reachability and parity objectives on RMDPs without making any assumption over the structures of the RMDPs, e.g., unichain or aperiodic. Our contributions are twofold. We first present efficient algorithms with oracle access to uncertainty sets that solve qualitative problems of reachability and parity objectives. We then report experimental results demonstrating the effectiveness of our oracle-based approach on classical RMDP examples from the literature scaling up to thousands of states.

Quantified Linear and Polynomial Arithmetic Satisfiability via Template-based Skolemization

The problem of checking satisfiability of linear real arithmetic (LRA) and non-linear real arithmetic (NRA) formulas has broad applications, in particular, they are at the heart of logic-related applications such as logic for artificial intelligence, program analysis, etc. While there has been much work on checking satisfiability of unquantified LRA and NRA formulas, the problem of checking satisfiability of quantified LRA and NRA formulas remains a significant challenge. The main bottleneck in the existing methods is a computationally expensive quantifier elimination step. In this work, we propose a novel method for efficient quantifier elimination in quantified LRA and NRA formulas. We propose a template-based Skolemization approach, where we automatically synthesize linear/polynomial Skolem functions in order to eliminate quantifiers in the formula. The key technical ingredients in our approach are Positivstellens\"atze theorems from algebraic geometry, which allow for an efficient manipulation of polynomial inequalities. Our method offers a range of appealing theoretical properties combined with a strong practical performance. On the theory side, our method is sound, semi-complete, and runs in subexponential time and polynomial space, as opposed to existing sound and complete quantifier elimination methods that run in doubly-exponential time and at least exponential space. On the practical side, our experiments show superior performance compared to state-of-the-art SMT solvers in terms of the number of solved instances and runtime, both on LRA and on NRA benchmarks.

Solving Long-run Average Reward Robust MDPs via Stochastic Games

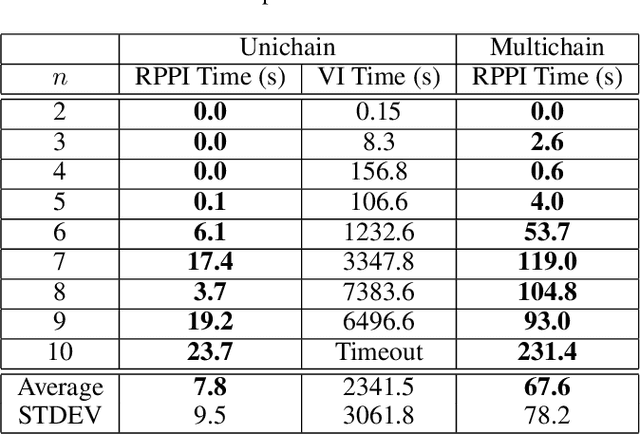
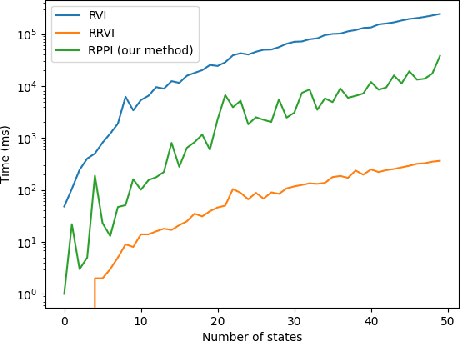
Markov decision processes (MDPs) provide a standard framework for sequential decision making under uncertainty. However, transition probabilities in MDPs are often estimated from data and MDPs do not take data uncertainty into account. Robust Markov decision processes (RMDPs) address this shortcoming of MDPs by assigning to each transition an uncertainty set rather than a single probability value. The goal of solving RMDPs is then to find a policy which maximizes the worst-case performance over the uncertainty sets. In this work, we consider polytopic RMDPs in which all uncertainty sets are polytopes and study the problem of solving long-run average reward polytopic RMDPs. Our focus is on computational complexity aspects and efficient algorithms. We present a novel perspective on this problem and show that it can be reduced to solving long-run average reward turn-based stochastic games with finite state and action spaces. This reduction allows us to derive several important consequences that were hitherto not known to hold for polytopic RMDPs. First, we derive new computational complexity bounds for solving long-run average reward polytopic RMDPs, showing for the first time that the threshold decision problem for them is in NP coNP and that they admit a randomized algorithm with sub-exponential expected runtime. Second, we present Robust Polytopic Policy Iteration (RPPI), a novel policy iteration algorithm for solving long-run average reward polytopic RMDPs. Our experimental evaluation shows that RPPI is much more efficient in solving long-run average reward polytopic RMDPs compared to state-of-the-art methods based on value iteration.