FORMS: Fine-grained Polarized ReRAM-based In-situ Computation for Mixed-signal DNN Accelerator

Recent works demonstrated the promise of using resistive random access memory (ReRAM) as an emerging technology to perform inherently parallel analog domain in-situ matrix-vector multiplication -- the intensive and key computation in DNNs. With weights stored in the ReRAM crossbar cells as conductance, when the input vector is applied to word lines, the matrix-vector multiplication results can be generated as the current in bit lines. A key problem is that the weight can be either positive or negative, but the in-situ computation assumes all cells on each crossbar column with the same sign. The current architectures either use two ReRAM crossbars for positive and negative weights, or add an offset to weights so that all values become positive. Neither solution is ideal: they either double the cost of crossbars, or incur extra offset circuity. To better solve this problem, this paper proposes FORMS, a fine-grained ReRAM-based DNN accelerator with polarized weights. Instead of trying to represent the positive/negative weights, our key design principle is to enforce exactly what is assumed in the in-situ computation -- ensuring that all weights in the same column of a crossbar have the same sign. It naturally avoids the cost of an additional crossbar. Such weights can be nicely generated using alternating direction method of multipliers (ADMM) regularized optimization, which can exactly enforce certain patterns in DNN weights. To achieve high accuracy, we propose to use fine-grained sub-array columns, which provide a unique opportunity for input zero-skipping, significantly avoiding unnecessary computations. It also makes the hardware much easier to implement. Putting all together, with the same optimized models, FORMS achieves significant throughput improvement and speed up in frame per second over ISAAC with similar area cost.

Rethinking Floating Point Overheads for Mixed Precision DNN Accelerators

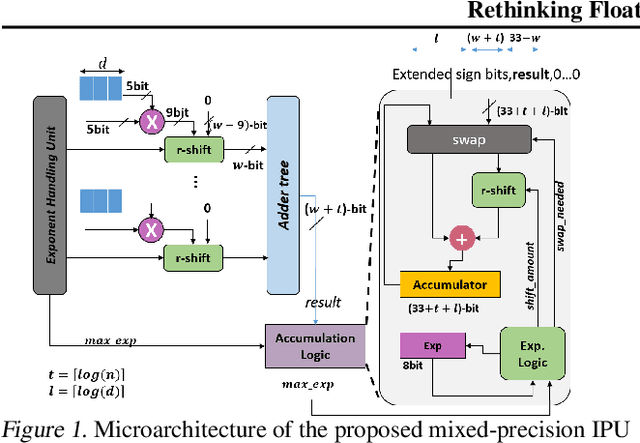
In this paper, we propose a mixed-precision convolution unit architecture which supports different integer and floating point (FP) precisions. The proposed architecture is based on low-bit inner product units and realizes higher precision based on temporal decomposition. We illustrate how to integrate FP computations on integer-based architecture and evaluate overheads incurred by FP arithmetic support. We argue that alignment and addition overhead for FP inner product can be significant since the maximum exponent difference could be up to 58 bits, which results into a large alignment logic. To address this issue, we illustrate empirically that no more than 26-bitproduct bits are required and up to 8-bit of alignment is sufficient in most inference cases. We present novel optimizations based on the above observations to reduce the FP arithmetic hardware overheads. Our empirical results, based on simulation and hardware implementation, show significant reduction in FP16 overhead. Over typical mixed precision implementation, the proposed architecture achieves area improvements of up to 25% in TFLOPS/mm2and up to 46% in TOPS/mm2with power efficiency improvements of up to 40% in TFLOPS/Wand up to 63% in TOPS/W.

Near-Lossless Post-Training Quantization of Deep Neural Networks via a Piecewise Linear Approximation

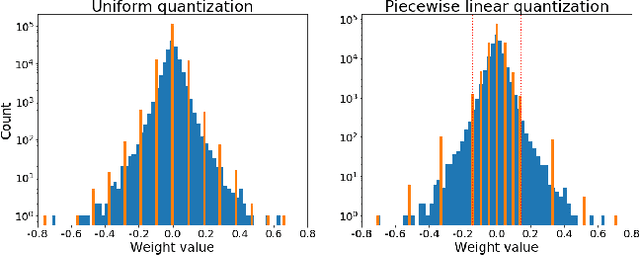
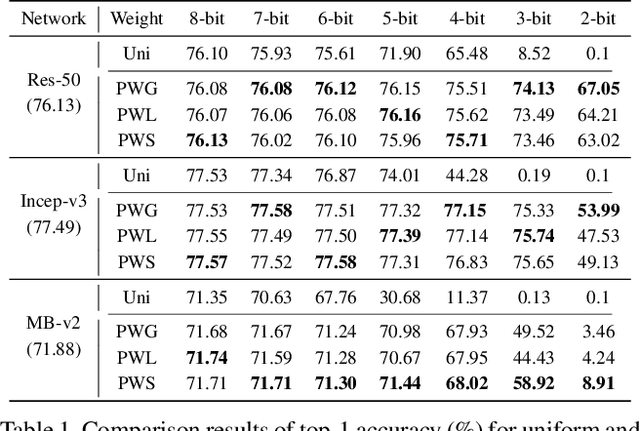
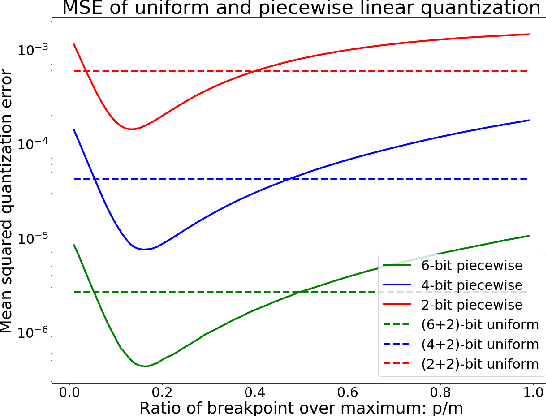
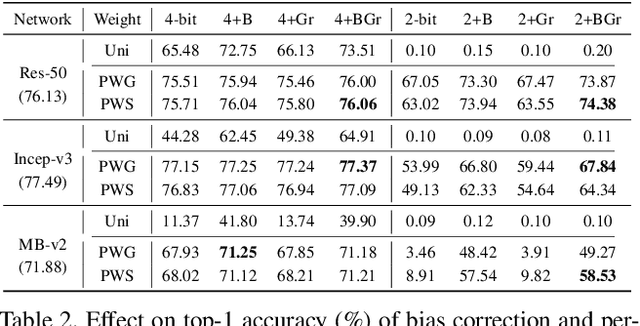
Quantization plays an important role for energy-efficient deployment of deep neural networks (DNNs) on resource-limited devices. Post-training quantization is crucial since it does not require retraining or accessibility to the full training dataset. The conventional post-training uniform quantization scheme achieves satisfactory results by converting DNNs from full-precision to 8-bit integers, however, it suffers from significant performance degradation when quantizing to lower precision such as 4 bits. In this paper, we propose a piecewise linear quantization method to enable accurate post-training quantization. Inspired from the fact that the weight tensors have bell-shaped distributions with long tails, our approach breaks the entire quantization range into two non-overlapping regions for each tensor, with each region being assigned an equal number of quantization levels. The optimal break-point that divides the entire range is found by minimizing the quantization error. Extensive results show that the proposed method achieves state-of-the-art performance on image classification, semantic segmentation and object detection. It is possible to quantize weights to 4 bits without retraining while nearly maintaining the performance of the original full-precision model.

Newton: Gravitating Towards the Physical Limits of Crossbar Acceleration

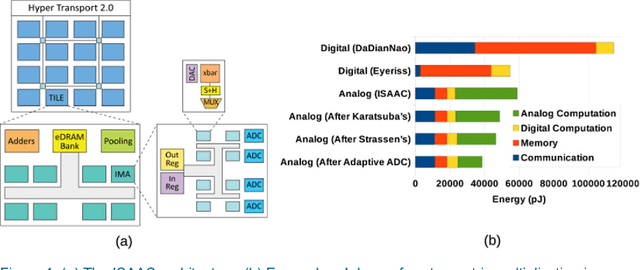
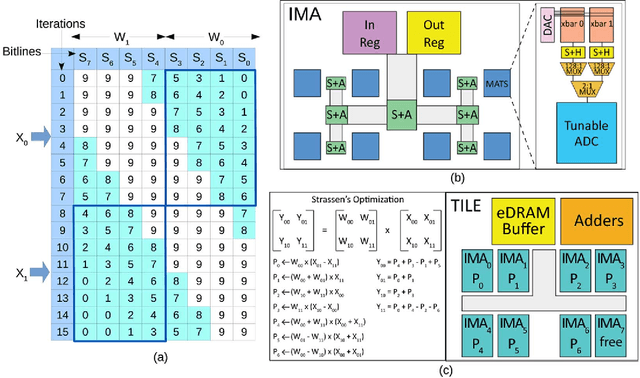
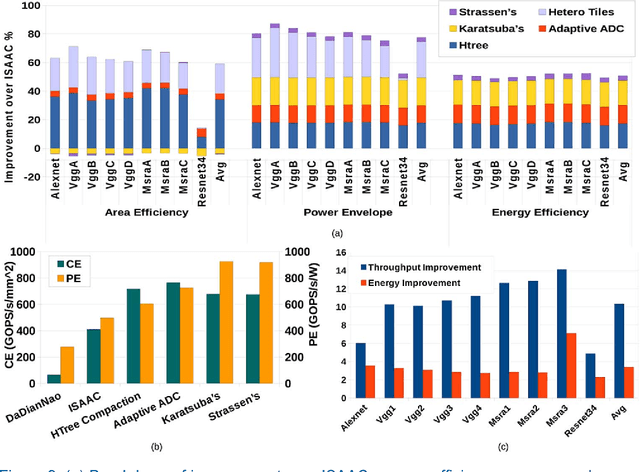
Many recent works have designed accelerators for Convolutional Neural Networks (CNNs). While digital accelerators have relied on near data processing, analog accelerators have further reduced data movement by performing in-situ computation. Recent works take advantage of highly parallel analog in-situ computation in memristor crossbars to accelerate the many vector-matrix multiplication operations in CNNs. However, these in-situ accelerators have two significant short-comings that we address in this work. First, the ADCs account for a large fraction of chip power and area. Second, these accelerators adopt a homogeneous design where every resource is provisioned for the worst case. By addressing both problems, the new architecture, Newton, moves closer to achieving optimal energy-per-neuron for crossbar accelerators. We introduce multiple new techniques that apply at different levels of the tile hierarchy. Two of the techniques leverage heterogeneity: one adapts ADC precision based on the requirements of every sub-computation (with zero impact on accuracy), and the other designs tiles customized for convolutions or classifiers. Two other techniques rely on divide-and-conquer numeric algorithms to reduce computations and ADC pressure. Finally, we place constraints on how a workload is mapped to tiles, thus helping reduce resource provisioning in tiles. For a wide range of CNN dataflows and structures, Newton achieves a 77% decrease in power, 51% improvement in energy efficiency, and 2.2x higher throughput/area, relative to the state-of-the-art ISAAC accelerator.