Rethinking Floating Point Overheads for Mixed Precision DNN Accelerators

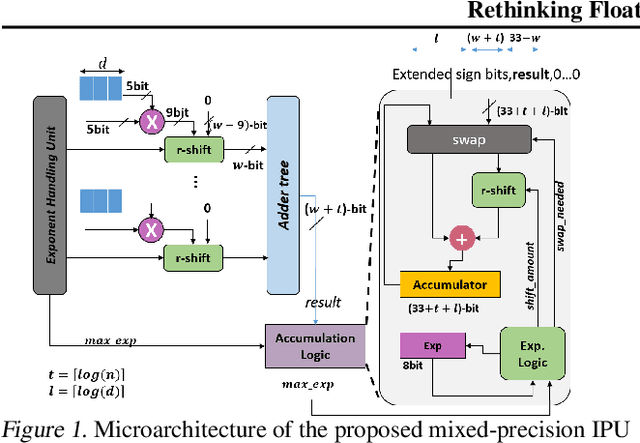
In this paper, we propose a mixed-precision convolution unit architecture which supports different integer and floating point (FP) precisions. The proposed architecture is based on low-bit inner product units and realizes higher precision based on temporal decomposition. We illustrate how to integrate FP computations on integer-based architecture and evaluate overheads incurred by FP arithmetic support. We argue that alignment and addition overhead for FP inner product can be significant since the maximum exponent difference could be up to 58 bits, which results into a large alignment logic. To address this issue, we illustrate empirically that no more than 26-bitproduct bits are required and up to 8-bit of alignment is sufficient in most inference cases. We present novel optimizations based on the above observations to reduce the FP arithmetic hardware overheads. Our empirical results, based on simulation and hardware implementation, show significant reduction in FP16 overhead. Over typical mixed precision implementation, the proposed architecture achieves area improvements of up to 25% in TFLOPS/mm2and up to 46% in TOPS/mm2with power efficiency improvements of up to 40% in TFLOPS/Wand up to 63% in TOPS/W.

Near-Lossless Post-Training Quantization of Deep Neural Networks via a Piecewise Linear Approximation

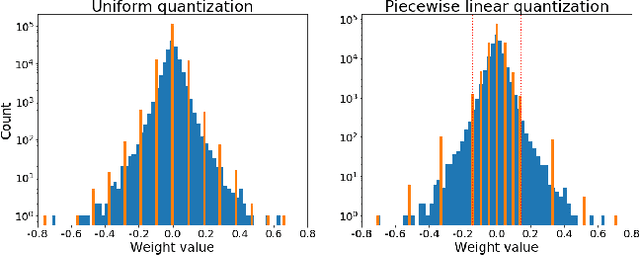
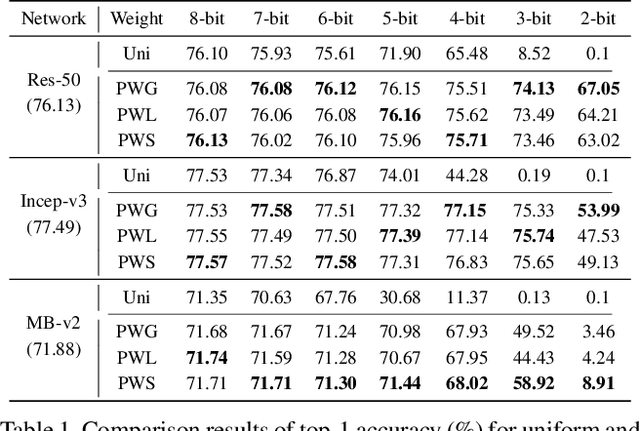
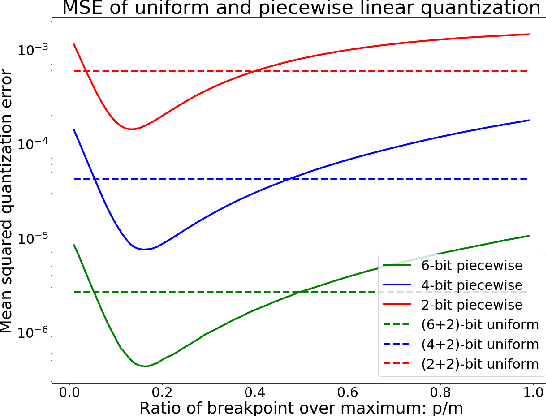
Quantization plays an important role for energy-efficient deployment of deep neural networks (DNNs) on resource-limited devices. Post-training quantization is crucial since it does not require retraining or accessibility to the full training dataset. The conventional post-training uniform quantization scheme achieves satisfactory results by converting DNNs from full-precision to 8-bit integers, however, it suffers from significant performance degradation when quantizing to lower precision such as 4 bits. In this paper, we propose a piecewise linear quantization method to enable accurate post-training quantization. Inspired from the fact that the weight tensors have bell-shaped distributions with long tails, our approach breaks the entire quantization range into two non-overlapping regions for each tensor, with each region being assigned an equal number of quantization levels. The optimal break-point that divides the entire range is found by minimizing the quantization error. Extensive results show that the proposed method achieves state-of-the-art performance on image classification, semantic segmentation and object detection. It is possible to quantize weights to 4 bits without retraining while nearly maintaining the performance of the original full-precision model.