Projected Model Counting: Beyond Independent Support
Paper and Code
Oct 18, 2021

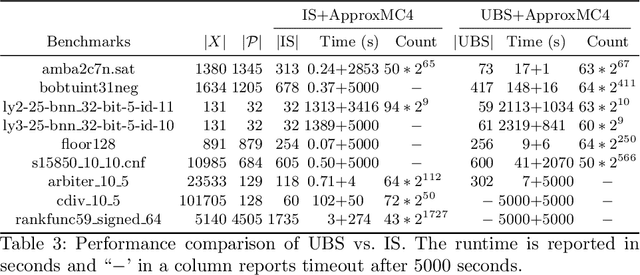
The past decade has witnessed a surge of interest in practical techniques for projected model counting. Despite significant advancements, however, performance scaling remains the Achilles' heel of this field. A key idea used in modern counters is to count models projected on an \emph{independent support} that is often a small subset of the projection set, i.e. original set of variables on which we wanted to project. While this idea has been effective in scaling performance, the question of whether it can benefit to count models projected on variables beyond the projection set, has not been explored. In this paper, we study this question and show that contrary to intuition, it can be beneficial to project on variables beyond the projection set. In applications such as verification of binarized neural networks, quantification of information flow, reliability of power grids etc., a good upper bound of the projected model count often suffices. We show that in several such cases, we can identify a set of variables, called upper bound support (UBS), that is not necessarily a subset of the projection set, and yet counting models projected on UBS guarantees an upper bound of the true projected model count. Theoretically, a UBS can be exponentially smaller than the smallest independent support. Our experiments show that even otherwise, UBS-based projected counting can be more efficient than independent support-based projected counting, while yielding bounds of very high quality. Based on extensive experiments, we find that UBS-based projected counting can solve many problem instances that are beyond the reach of a state-of-the-art independent support-based projected model counter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge