Formally Certified Approximate Model Counting

Approximate model counting is the task of approximating the number of solutions to an input Boolean formula. The state-of-the-art approximate model counter for formulas in conjunctive normal form (CNF), ApproxMC, provides a scalable means of obtaining model counts with probably approximately correct (PAC)-style guarantees. Nevertheless, the validity of ApproxMC's approximation relies on a careful theoretical analysis of its randomized algorithm and the correctness of its highly optimized implementation, especially the latter's stateful interactions with an incremental CNF satisfiability solver capable of natively handling parity (XOR) constraints. We present the first certification framework for approximate model counting with formally verified guarantees on the quality of its output approximation. Our approach combines: (i) a static, once-off, formal proof of the algorithm's PAC guarantee in the Isabelle/HOL proof assistant; and (ii) dynamic, per-run, verification of ApproxMC's calls to an external CNF-XOR solver using proof certificates. We detail our general approach to establish a rigorous connection between these two parts of the verification, including our blueprint for turning the formalized, randomized algorithm into a verified proof checker, and our design of proof certificates for both ApproxMC and its internal CNF-XOR solving steps. Experimentally, we show that certificate generation adds little overhead to an approximate counter implementation, and that our certificate checker is able to fully certify $84.7\%$ of instances with generated certificates when given the same time and memory limits as the counter.

Explaining SAT Solving Using Causal Reasoning

The past three decades have witnessed notable success in designing efficient SAT solvers, with modern solvers capable of solving industrial benchmarks containing millions of variables in just a few seconds. The success of modern SAT solvers owes to the widely-used CDCL algorithm, which lacks comprehensive theoretical investigation. Furthermore, it has been observed that CDCL solvers still struggle to deal with specific classes of benchmarks comprising only hundreds of variables, which contrasts with their widespread use in real-world applications. Consequently, there is an urgent need to uncover the inner workings of these seemingly weak yet powerful black boxes. In this paper, we present a first step towards this goal by introducing an approach called CausalSAT, which employs causal reasoning to gain insights into the functioning of modern SAT solvers. CausalSAT initially generates observational data from the execution of SAT solvers and learns a structured graph representing the causal relationships between the components of a SAT solver. Subsequently, given a query such as whether a clause with low literals blocks distance (LBD) has a higher clause utility, CausalSAT calculates the causal effect of LBD on clause utility and provides an answer to the question. We use CausalSAT to quantitatively verify hypotheses previously regarded as "rules of thumb" or empirical findings such as the query above. Moreover, CausalSAT can address previously unexplored questions, like which branching heuristic leads to greater clause utility in order to study the relationship between branching and clause management. Experimental evaluations using practical benchmarks demonstrate that CausalSAT effectively fits the data, verifies four "rules of thumb", and provides answers to three questions closely related to implementing modern solvers.

Arjun: An Efficient Independent Support Computation Technique and its Applications to Counting and Sampling

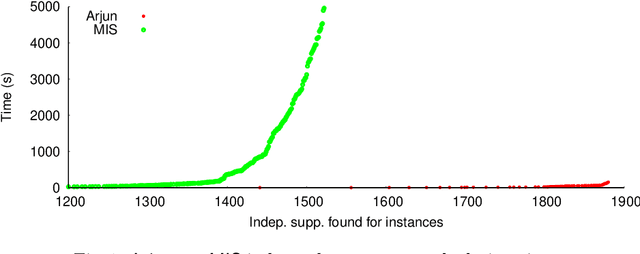
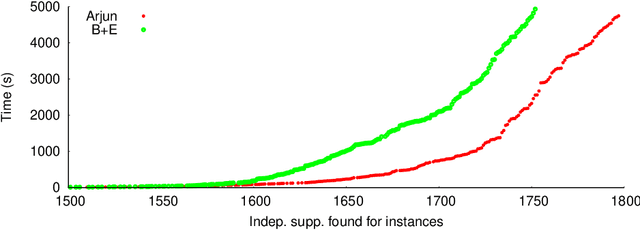
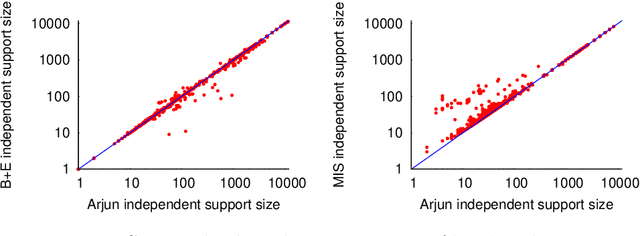
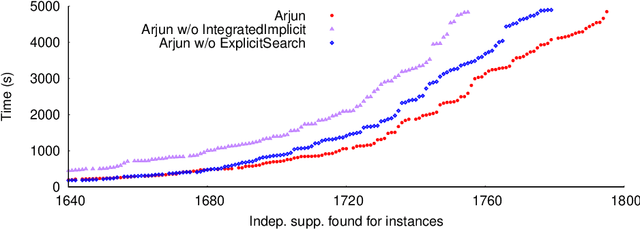
Given a Boolean formula $\varphi$ over the set of variables $X$ and a projection set $\mathcal{P} \subseteq X$, a subset of variables $\mathcal{I}$ is independent support of $\mathcal{P}$ if two solutions agree on $\mathcal{I}$, then they also agree on $\mathcal{P}$. The notion of independent support is related to the classical notion of definability dating back to 1901, and have been studied over the decades. Recently, the computational problem of determining independent support for a given formula has attained importance owing to the crucial importance of independent support for hashing-based counting and sampling techniques. In this paper, we design an efficient and scalable independent support computation technique that can handle formulas arising from real-world benchmarks. Our algorithmic framework, called Arjun, employs implicit and explicit definability notions, and is based on a tight integration of gate-identification techniques and assumption-based framework. We demonstrate that augmenting the state of the art model counter ApproxMC4 and sampler UniGen3 with Arjun leads to significant performance improvements. In particular, ApproxMC4 augmented with Arjun counts 387 more benchmarks out of 1896 while UniGen3 augmented with Arjun samples 319 more benchmarks within the same time limit.