The Cardinality of Identifying Code Sets for Soccer Ball Graph with Application to Remote Sensing

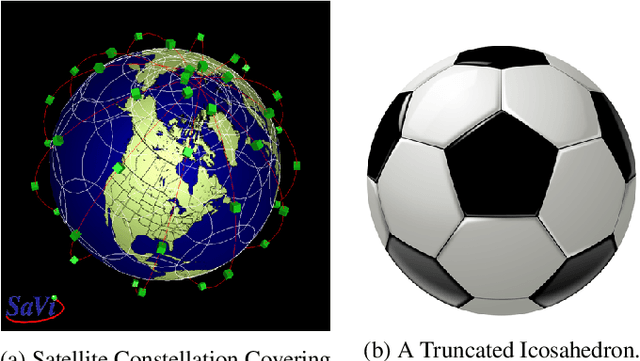
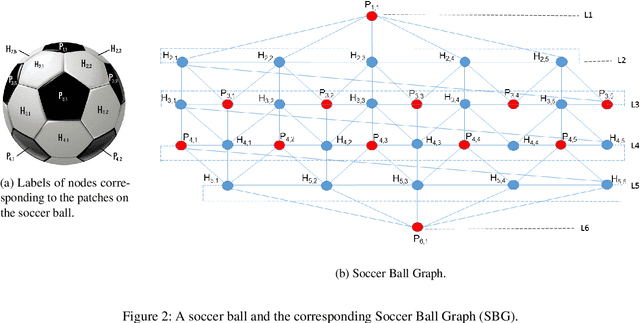
In the context of satellite monitoring of the earth, we can assume that the surface of the earth is divided into a set of regions. We assume that the impact of a big social/environmental event spills into neighboring regions. Using Identifying Code Sets (ICSes), we can deploy sensors in such a way that the region in which an event takes place can be uniquely identified, even with fewer sensors than regions. As Earth is almost a sphere, we use a soccer ball as a model. We construct a Soccer Ball Graph (SBG), and provide human-oriented, analytical proofs that 1) the SBG has at least 26 ICSes of cardinality ten, implying that there are at least 26 different ways to deploy ten satellites to monitor the Earth and 2) that the cardinality of the minimum Identifying Code Set (MICS) for the SBG is at least nine. We then provide a machine-oriented formal proof that the cardinality of the MICS for the SBG is in fact ten, meaning that one must deploy at least ten satellites to monitor the Earth in the SBG model. We also provide machine-oriented proof that there are exactly 26 ICSes of cardinality ten for the SBG.