Interpretable DNFs

A classifier is considered interpretable if each of its decisions has an explanation which is small enough to be easily understood by a human user. A DNF formula can be seen as a binary classifier $\kappa$ over boolean domains. The size of an explanation of a positive decision taken by a DNF $\kappa$ is bounded by the size of the terms in $\kappa$, since we can explain a positive decision by giving a term of $\kappa$ that evaluates to true. Since both positive and negative decisions must be explained, we consider that interpretable DNFs are those $\kappa$ for which both $\kappa$ and $\overline{\kappa}$ can be expressed as DNFs composed of terms of bounded size. In this paper, we study the family of $k$-DNFs whose complements can also be expressed as $k$-DNFs. We compare two such families, namely depth-$k$ decision trees and nested $k$-DNFs, a novel family of models. Experiments indicate that nested $k$-DNFs are an interesting alternative to decision trees in terms of interpretability and accuracy.

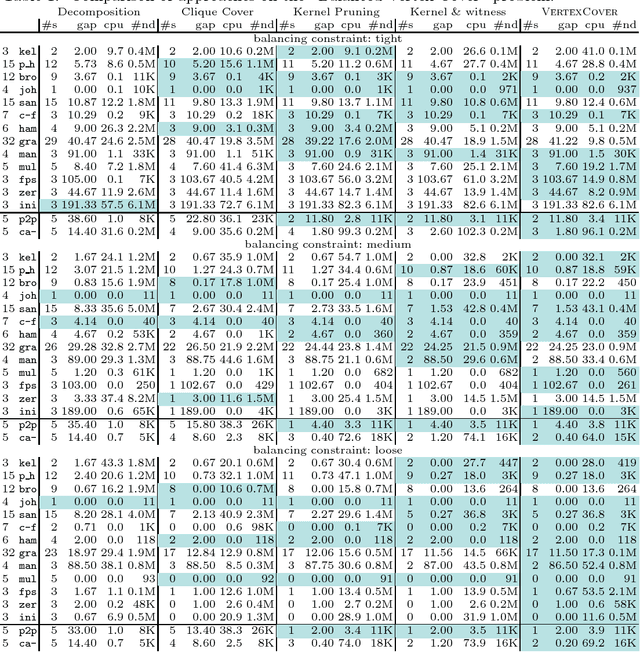
Propagation via Kernelization: The Vertex Cover Constraint

The technique of kernelization consists in extracting, from an instance of a problem, an essentially equivalent instance whose size is bounded in a parameter k. Besides being the basis for efficient param-eterized algorithms, this method also provides a wealth of information to reason about in the context of constraint programming. We study the use of kernelization for designing propagators through the example of the Vertex Cover constraint. Since the classic kernelization rules often correspond to dominance rather than consistency, we introduce the notion of "loss-less" kernel. While our preliminary experimental results show the potential of the approach, they also show some of its limits. In particular, this method is more effective for vertex covers of large and sparse graphs, as they tend to have, relatively, smaller kernels.

The Dichotomy for Conservative Constraint Satisfaction is Polynomially Decidable

Given a fixed constraint language $\Gamma$, the conservative CSP over $\Gamma$ (denoted by c-CSP($\Gamma$)) is a variant of CSP($\Gamma$) where the domain of each variable can be restricted arbitrarily. A dichotomy is known for conservative CSP: for every fixed language $\Gamma$, c-CSP($\Gamma$) is either in P or NP-complete. However, the characterization of conservatively tractable languages is of algebraic nature and the naive recognition algorithm is super-exponential in the domain size. The main contribution of this paper is a polynomial-time algorithm that, given a constraint language $\Gamma$ as input, decides if c-CSP($\Gamma$) is tractable. In addition, if $\Gamma$ is proven tractable the algorithm also outputs its coloured graph, which contains valuable information on the structure of $\Gamma$.