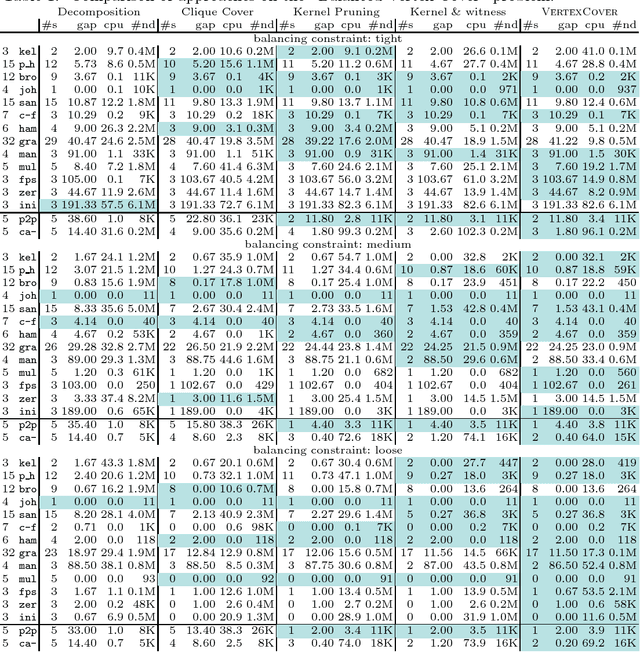
Propagation via Kernelization: The Vertex Cover Constraint

The technique of kernelization consists in extracting, from an instance of a problem, an essentially equivalent instance whose size is bounded in a parameter k. Besides being the basis for efficient param-eterized algorithms, this method also provides a wealth of information to reason about in the context of constraint programming. We study the use of kernelization for designing propagators through the example of the Vertex Cover constraint. Since the classic kernelization rules often correspond to dominance rather than consistency, we introduce the notion of "loss-less" kernel. While our preliminary experimental results show the potential of the approach, they also show some of its limits. In particular, this method is more effective for vertex covers of large and sparse graphs, as they tend to have, relatively, smaller kernels.

Constraint programming for planning test campaigns of communications satellites

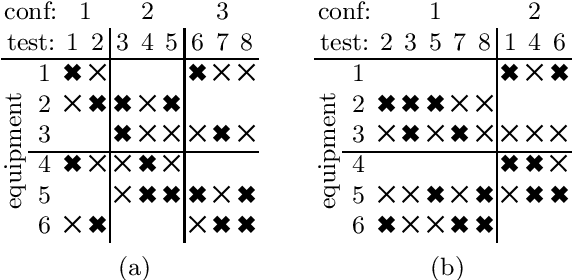
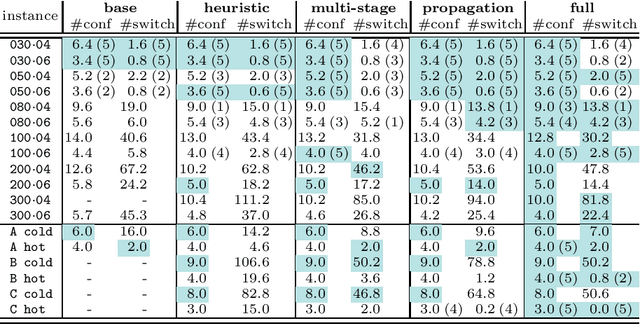
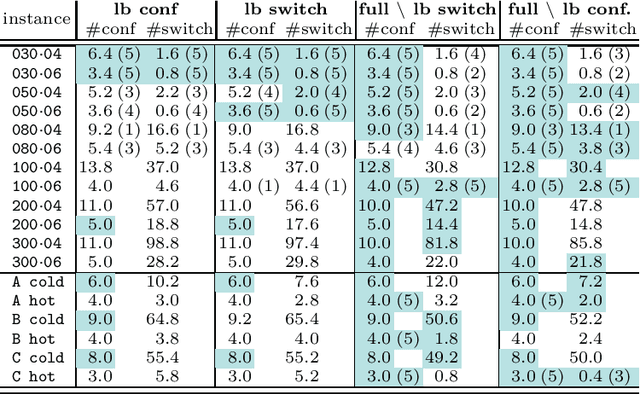
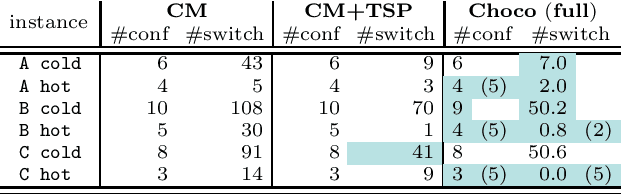
The payload of communications satellites must go through a series of tests to assert their ability to survive in space. Each test involves some equipment of the payload to be active, which has an impact on the temperature of the payload. Sequencing these tests in a way that ensures the thermal stability of the payload and minimizes the overall duration of the test campaign is a very important objective for satellite manufacturers. The problem can be decomposed in two sub-problems corresponding to two objectives: First, the number of distinct configurations necessary to run the tests must be minimized. This can be modeled as packing the tests into configurations, and we introduce a set of implied constraints to improve the lower bound of the model. Second, tests must be sequenced so that the number of times an equipment unit has to be switched on or off is minimized. We model this aspect using the constraint Switch, where a buffer with limited capacity represents the currently active equipment units, and we introduce an improvement of the propagation algorithm for this constraint. We then introduce a search strategy in which we sequentially solve the sub-problems (packing and sequencing). Experiments conducted on real and random instances show the respective interest of our contributions.