From Matching with Diversity Constraints to Matching with Regional Quotas

In the past few years, several new matching models have been proposed and studied that take into account complex distributional constraints. Relevant lines of work include (1) school choice with diversity constraints where students have (possibly overlapping) types and (2) hospital-doctor matching where various regional quotas are imposed. In this paper, we present a polynomial-time reduction to transform an instance of (1) to an instance of (2) and we show how the feasibility and stability of corresponding matchings are preserved under the reduction. Our reduction provides a formal connection between two important strands of work on matching with distributional constraints. We then apply the reduction in two ways. Firstly, we show that it is NP-complete to check whether a feasible and stable outcome for (1) exists. Due to our reduction, these NP-completeness results carry over to setting (2). In view of this, we help unify some of the results that have been presented in the literature. Secondly, if we have positive results for (2), then we have corresponding results for (1). One key conclusion of our results is that further developments on axiomatic and algorithmic aspects of hospital-doctor matching with regional quotas will result in corresponding results for school choice with diversity constraints.

Backdoors into Heterogeneous Classes of SAT and CSP

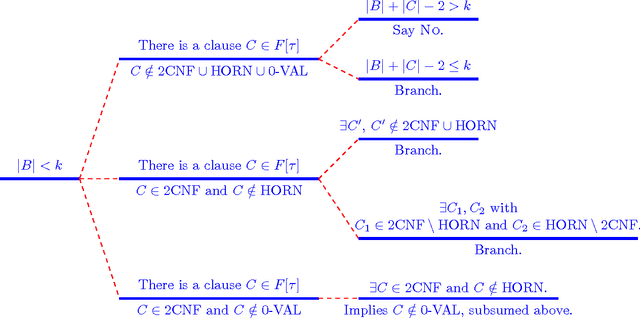
In this paper we extend the classical notion of strong and weak backdoor sets for SAT and CSP by allowing that different instantiations of the backdoor variables result in instances that belong to different base classes; the union of the base classes forms a heterogeneous base class. Backdoor sets to heterogeneous base classes can be much smaller than backdoor sets to homogeneous ones, hence they are much more desirable but possibly harder to find. We draw a detailed complexity landscape for the problem of detecting strong and weak backdoor sets into heterogeneous base classes for SAT and CSP.

Interdependent Scheduling Games

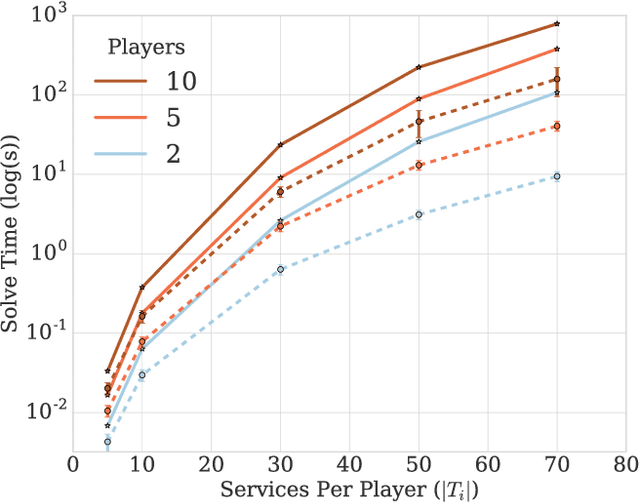
We propose a model of interdependent scheduling games in which each player controls a set of services that they schedule independently. A player is free to schedule his own services at any time; however, each of these services only begins to accrue reward for the player when all predecessor services, which may or may not be controlled by the same player, have been activated. This model, where players have interdependent services, is motivated by the problems faced in planning and coordinating large-scale infrastructures, e.g., restoring electricity and gas to residents after a natural disaster or providing medical care in a crisis when different agencies are responsible for the delivery of staff, equipment, and medicine. We undertake a game-theoretic analysis of this setting and in particular consider the issues of welfare maximization, computing best responses, Nash dynamics, and existence and computation of Nash equilibria.

Fair assignment of indivisible objects under ordinal preferences

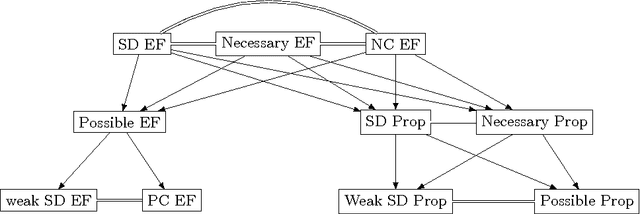
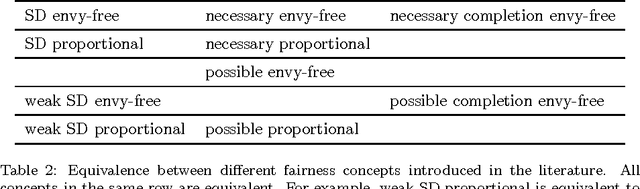
We consider the discrete assignment problem in which agents express ordinal preferences over objects and these objects are allocated to the agents in a fair manner. We use the stochastic dominance relation between fractional or randomized allocations to systematically define varying notions of proportionality and envy-freeness for discrete assignments. The computational complexity of checking whether a fair assignment exists is studied for these fairness notions. We also characterize the conditions under which a fair assignment is guaranteed to exist. For a number of fairness concepts, polynomial-time algorithms are presented to check whether a fair assignment exists. Our algorithmic results also extend to the case of unequal entitlements of agents. Our NP-hardness result, which holds for several variants of envy-freeness, answers an open question posed by Bouveret, Endriss, and Lang (ECAI 2010). We also propose fairness concepts that always suggest a non-empty set of assignments with meaningful fairness properties. Among these concepts, optimal proportionality and optimal weak proportionality appear to be desirable fairness concepts.

Online Fair Division: analysing a Food Bank problem

We study an online model of fair division designed to capture features of a real world charity problem. We consider two simple mechanisms for this model in which agents simply declare what items they like. We analyse several axiomatic properties of these mechanisms like strategy-proofness and envy-freeness. Finally, we perform a competitive analysis and compute the price of anarchy.

Computational Aspects of Multi-Winner Approval Voting

We study computational aspects of three prominent voting rules that use approval ballots to elect multiple winners. These rules are satisfaction approval voting, proportional approval voting, and reweighted approval voting. We first show that computing the winner for proportional approval voting is NP-hard, closing a long standing open problem. As none of the rules are strategyproof, even for dichotomous preferences, we study various strategic aspects of the rules. In particular, we examine the computational complexity of computing a best response for both a single agent and a group of agents. In many settings, we show that it is NP-hard for an agent or agents to compute how best to vote given a fixed set of approval ballots from the other agents.

Guarantees and Limits of Preprocessing in Constraint Satisfaction and Reasoning

We present a first theoretical analysis of the power of polynomial-time preprocessing for important combinatorial problems from various areas in AI. We consider problems from Constraint Satisfaction, Global Constraints, Satisfiability, Nonmonotonic and Bayesian Reasoning under structural restrictions. All these problems involve two tasks: (i) identifying the structure in the input as required by the restriction, and (ii) using the identified structure to solve the reasoning task efficiently. We show that for most of the considered problems, task (i) admits a polynomial-time preprocessing to a problem kernel whose size is polynomial in a structural problem parameter of the input, in contrast to task (ii) which does not admit such a reduction to a problem kernel of polynomial size, subject to a complexity theoretic assumption. As a notable exception we show that the consistency problem for the AtMost-NValue constraint admits a polynomial kernel consisting of a quadratic number of variables and domain values. Our results provide a firm worst-case guarantees and theoretical boundaries for the performance of polynomial-time preprocessing algorithms for the considered problems.

Coalitional Manipulation for Schulze's Rule

Schulze's rule is used in the elections of a large number of organizations including Wikimedia and Debian. Part of the reason for its popularity is the large number of axiomatic properties, like monotonicity and Condorcet consistency, which it satisfies. We identify a potential shortcoming of Schulze's rule: it is computationally vulnerable to manipulation. In particular, we prove that computing an unweighted coalitional manipulation (UCM) is polynomial for any number of manipulators. This result holds for both the unique winner and the co-winner versions of UCM. This resolves an open question stated by Parkes and Xia (2012). We also prove that computing a weighted coalitional manipulation (WCM) is polynomial for a bounded number of candidates. Finally, we discuss the relation between the unique winner UCM problem and the co-winner UCM problem and argue that they have substantially different necessary and sufficient conditions for the existence of a successful manipulation.

Possible and Necessary Winner Problem in Social Polls

Social networks are increasingly being used to conduct polls. We introduce a simple model of such social polling. We suppose agents vote sequentially, but the order in which agents choose to vote is not necessarily fixed. We also suppose that an agent's vote is influenced by the votes of their friends who have already voted. Despite its simplicity, this model provides useful insights into a number of areas including social polling, sequential voting, and manipulation. We prove that the number of candidates and the network structure affect the computational complexity of computing which candidate necessarily or possibly can win in such a social poll. For social networks with bounded treewidth and a bounded number of candidates, we provide polynomial algorithms for both problems. In other cases, we prove that computing which candidates necessarily or possibly win are computationally intractable.

On Finding Optimal Polytrees

Inferring probabilistic networks from data is a notoriously difficult task. Under various goodness-of-fit measures, finding an optimal network is NP-hard, even if restricted to polytrees of bounded in-degree. Polynomial-time algorithms are known only for rare special cases, perhaps most notably for branchings, that is, polytrees in which the in-degree of every node is at most one. Here, we study the complexity of finding an optimal polytree that can be turned into a branching by deleting some number of arcs or nodes, treated as a parameter. We show that the problem can be solved via a matroid intersection formulation in polynomial time if the number of deleted arcs is bounded by a constant. The order of the polynomial time bound depends on this constant, hence the algorithm does not establish fixed-parameter tractability when parameterized by the number of deleted arcs. We show that a restricted version of the problem allows fixed-parameter tractability and hence scales well with the parameter. We contrast this positive result by showing that if we parameterize by the number of deleted nodes, a somewhat more powerful parameter, the problem is not fixed-parameter tractable, subject to a complexity-theoretic assumption.