TReR: A Lightweight Transformer Re-Ranking Approach for 3D LiDAR Place Recognition

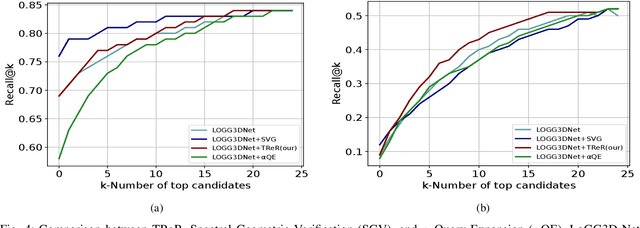
Autonomous driving systems often require reliable loop closure detection to guarantee reduced localization drift. Recently, 3D LiDAR-based localization methods have used retrieval-based place recognition to find revisited places efficiently. However, when deployed in challenging real-world scenarios, the place recognition models become more complex, which comes at the cost of high computational demand. This work tackles this problem from an information-retrieval perspective, adopting a first-retrieve-then-re-ranking paradigm, where an initial loop candidate ranking, generated from a 3D place recognition model, is re-ordered by a proposed lightweight transformer-based re-ranking approach (TReR). The proposed approach relies on global descriptors only, being agnostic to the place recognition model. The experimental evaluation, conducted on the KITTI Odometry dataset, where we compared TReR with s.o.t.a. re-ranking approaches such as alphaQE and SGV, indicate the robustness and efficiency when compared to alphaQE while offering a good trade-off between robustness and efficiency when compared to SGV.

Envy-freeness up to one item: Shall we add or remove resources?

We consider a fair division model in which agents have general valuations for bundles of indivisible items. We propose two new axiomatic properties for allocations in this model: EF1+- and EFX+-. We compare these with the existing EF1 and EFX. Although EF1 and EF1+- allocations often exist, our results assert eloquently that EFX+- and PO allocations exist in each case where EFX and PO allocations do not exist. Additionally, we prove several new impossibility and incompatibility results.

Jealousy-freeness and other common properties in Fair Division of Mixed Manna

We consider a fair division setting where indivisible items are allocated to agents. Each agent in the setting has strictly negative, zero or strictly positive utility for each item. We, thus, make a distinction between items that are good for some agents and bad for other agents (i.e. mixed), good for everyone (i.e. goods) or bad for everyone (i.e. bads). For this model, we study axiomatic concepts of allocations such as jealousy-freeness up to one item, envy-freeness up to one item and Pareto-optimality. We obtain many new possibility and impossibility results in regard to combinations of these properties. We also investigate new computational tasks related to such combinations. Thus, we advance the state-of-the-art in fair division of mixed manna.

Greedy Algorithms for Fair Division of Mixed Manna

We consider a multi-agent model for fair division of mixed manna (i.e. items for which agents can have positive, zero or negative utilities), in which agents have additive utilities for bundles of items. For this model, we give several general impossibility results and special possibility results for three common fairness concepts (i.e. EF1, EFX, EFX3) and one popular efficiency concept (i.e. PO). We also study how these interact with common welfare objectives such as the Nash, disutility Nash and egalitarian welfares. For example, we show that maximizing the Nash welfare with mixed manna (or minimizing the disutility Nash welfare) does not ensure an EF1 allocation whereas with goods and the Nash welfare it does. We also prove that an EFX3 allocation may not exist even with identical utilities. By comparison, with tertiary utilities, EFX and PO allocations, or EFX3 and PO allocations always exist. Also, with identical utilities, EFX and PO allocations always exist. For these cases, we give polynomial-time algorithms, returning such allocations and approximating further the Nash, disutility Nash and egalitarian welfares in special cases.

Online Fair Division: A Survey

We survey a burgeoning and promising new research area that considers the online nature of many practical fair division problems. We identify wide variety of such online fair division problems, as well as discuss new mechanisms and normative properties that apply to this online setting. The online nature of such fair division problems provides both opportunities and challenges such as the possibility to develop new online mechanisms as well as the difficulty of dealing with an uncertain future.

Online Fair Division: analysing a Food Bank problem

We study an online model of fair division designed to capture features of a real world charity problem. We consider two simple mechanisms for this model in which agents simply declare what items they like. We analyse several axiomatic properties of these mechanisms like strategy-proofness and envy-freeness. Finally, we perform a competitive analysis and compute the price of anarchy.