The Provable Virtue of Laziness in Motion Planning

The Lazy Shortest Path (LazySP) class consists of motion-planning algorithms that only evaluate edges along shortest paths between the source and target. These algorithms were designed to minimize the number of edge evaluations in settings where edge evaluation dominates the running time of the algorithm; but how close to optimal are LazySP algorithms in terms of this objective? Our main result is an analytical upper bound, in a probabilistic model, on the number of edge evaluations required by LazySP algorithms; a matching lower bound shows that these algorithms are asymptotically optimal in the worst case.

A Discrete and Bounded Envy-Free Cake Cutting Protocol for Any Number of Agents

We consider the well-studied cake cutting problem in which the goal is to find an envy-free allocation based on queries from $n$ agents. The problem has received attention in computer science, mathematics, and economics. It has been a major open problem whether there exists a discrete and bounded envy-free protocol. We resolve the problem by proposing a discrete and bounded envy-free protocol for any number of agents. The maximum number of queries required by the protocol is $n^{n^{n^{n^{n^n}}}}$. We additionally show that even if we do not run our protocol to completion, it can find in at most $n^3{(n^2)}^n$ queries a partial allocation of the cake that achieves proportionality (each agent gets at least $1/n$ of the value of the whole cake) and envy-freeness. Finally we show that an envy-free partial allocation can be computed in at most $n^3{(n^2)}^n$ queries such that each agent gets a connected piece that gives the agent at least $1/(3n)$ of the value of the whole cake.

Fair assignment of indivisible objects under ordinal preferences

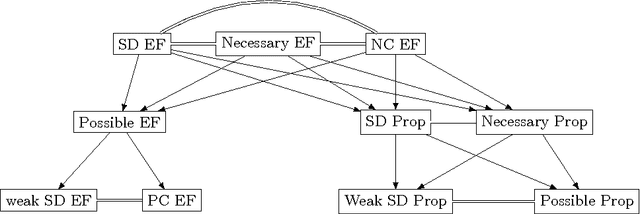
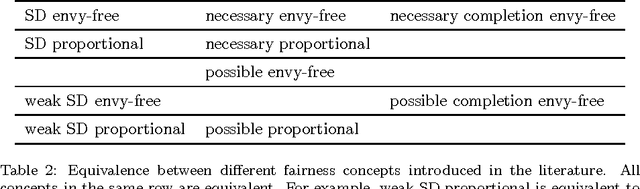
We consider the discrete assignment problem in which agents express ordinal preferences over objects and these objects are allocated to the agents in a fair manner. We use the stochastic dominance relation between fractional or randomized allocations to systematically define varying notions of proportionality and envy-freeness for discrete assignments. The computational complexity of checking whether a fair assignment exists is studied for these fairness notions. We also characterize the conditions under which a fair assignment is guaranteed to exist. For a number of fairness concepts, polynomial-time algorithms are presented to check whether a fair assignment exists. Our algorithmic results also extend to the case of unequal entitlements of agents. Our NP-hardness result, which holds for several variants of envy-freeness, answers an open question posed by Bouveret, Endriss, and Lang (ECAI 2010). We also propose fairness concepts that always suggest a non-empty set of assignments with meaningful fairness properties. Among these concepts, optimal proportionality and optimal weak proportionality appear to be desirable fairness concepts.

Computational Aspects of Multi-Winner Approval Voting

We study computational aspects of three prominent voting rules that use approval ballots to elect multiple winners. These rules are satisfaction approval voting, proportional approval voting, and reweighted approval voting. We first show that computing the winner for proportional approval voting is NP-hard, closing a long standing open problem. As none of the rules are strategyproof, even for dichotomous preferences, we study various strategic aspects of the rules. In particular, we examine the computational complexity of computing a best response for both a single agent and a group of agents. In many settings, we show that it is NP-hard for an agent or agents to compute how best to vote given a fixed set of approval ballots from the other agents.