Thomas Kalinowski
Welfare of Sequential Allocation Mechanisms for Indivisible Goods
Nov 26, 2015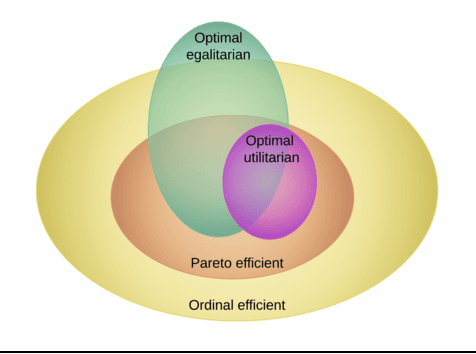

Abstract:Sequential allocation is a simple and attractive mechanism for the allocation of indivisible goods. Agents take turns, according to a policy, to pick items. Sequential allocation is guaranteed to return an allocation which is efficient but may not have an optimal social welfare. We consider therefore the relation between welfare and efficiency. We study the (computational) questions of what welfare is possible or necessary depending on the choice of policy. We also consider a novel control problem in which the chair chooses a policy to improve social welfare.
A Social Welfare Optimal Sequential Allocation Procedure
Apr 23, 2013



Abstract:We consider a simple sequential allocation procedure for sharing indivisible items between agents in which agents take turns to pick items. Supposing additive utilities and independence between the agents, we show that the expected utility of each agent is computable in polynomial time. Using this result, we prove that the expected utilitarian social welfare is maximized when agents take alternate turns. We also argue that this mechanism remains optimal when agents behave strategically
Coalitional Manipulation for Schulze's Rule
Apr 03, 2013



Abstract:Schulze's rule is used in the elections of a large number of organizations including Wikimedia and Debian. Part of the reason for its popularity is the large number of axiomatic properties, like monotonicity and Condorcet consistency, which it satisfies. We identify a potential shortcoming of Schulze's rule: it is computationally vulnerable to manipulation. In particular, we prove that computing an unweighted coalitional manipulation (UCM) is polynomial for any number of manipulators. This result holds for both the unique winner and the co-winner versions of UCM. This resolves an open question stated by Parkes and Xia (2012). We also prove that computing a weighted coalitional manipulation (WCM) is polynomial for a bounded number of candidates. Finally, we discuss the relation between the unique winner UCM problem and the co-winner UCM problem and argue that they have substantially different necessary and sufficient conditions for the existence of a successful manipulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge