Average-Case Analysis of Iterative Voting

Iterative voting is a natural model of repeated strategic decision-making in social choice when agents have the opportunity to update their votes prior to finalizing the group decision. Prior work has analyzed the efficacy of iterative plurality on the welfare of the chosen outcome at equilibrium, relative to the truthful vote profile, via an adaptation of the price of anarchy. However, prior analyses have only studied the worst-case and average-case performances when agents' preferences are distributed by the impartial culture. This work extends average-case analyses to a wider class of distributions and distinguishes when iterative plurality improves or degrades asymptotic welfare.

LLM-augmented Preference Learning from Natural Language

Finding preferences expressed in natural language is an important but challenging task. State-of-the-art(SotA) methods leverage transformer-based models such as BERT, RoBERTa, etc. and graph neural architectures such as graph attention networks. Since Large Language Models (LLMs) are equipped to deal with larger context lengths and have much larger model sizes than the transformer-based model, we investigate their ability to classify comparative text directly. This work aims to serve as a first step towards using LLMs for the CPC task. We design and conduct a set of experiments that format the classification task into an input prompt for the LLM and a methodology to get a fixed-format response that can be automatically evaluated. Comparing performances with existing methods, we see that pre-trained LLMs are able to outperform the previous SotA models with no fine-tuning involved. Our results show that the LLMs can consistently outperform the SotA when the target text is large -- i.e. composed of multiple sentences --, and are still comparable to the SotA performance in shorter text. We also find that few-shot learning yields better performance than zero-shot learning.

Determining Winners in Elections with Absent Votes

An important question in elections is the determine whether a candidate can be a winner when some votes are absent. We study this determining winner with the absent votes (WAV) problem when the votes are top-truncated. We show that the WAV problem is NP-complete for the single transferable vote, Maximin, and Copeland, and propose a special case of positional scoring rule such that the problem can be computed in polynomial time. Our results in top-truncated rankings differ from the results in full rankings as their hardness results still hold when the number of candidates or the number of missing votes are bounded, while we show that the problem can be solved in polynomial time in either case.

First-Choice Maximality Meets Ex-ante and Ex-post Fairness

For the assignment problem where multiple indivisible items are allocated to a group of agents given their ordinal preferences, we design randomized mechanisms that satisfy first-choice maximality (FCM), i.e., maximizing the number of agents assigned their first choices, together with Pareto efficiency (PE). Our mechanisms also provide guarantees of ex-ante and ex-post fairness. The generalized eager Boston mechanism is ex-ante envy-free, and ex-post envy-free up to one item (EF1). The generalized probabilistic Boston mechanism is also ex-post EF1, and satisfies ex-ante efficiency instead of fairness. We also show that no strategyproof mechanism satisfies ex-post PE, EF1, and FCM simultaneously. In doing so, we expand the frontiers of simultaneously providing efficiency and both ex-ante and ex-post fairness guarantees for the assignment problem.

Differentially Private Condorcet Voting

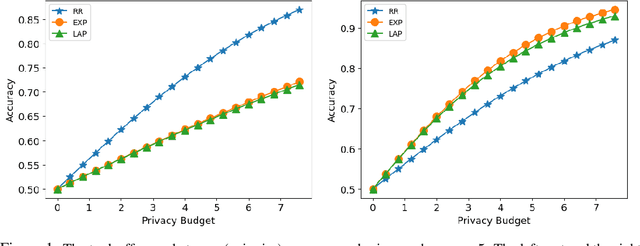
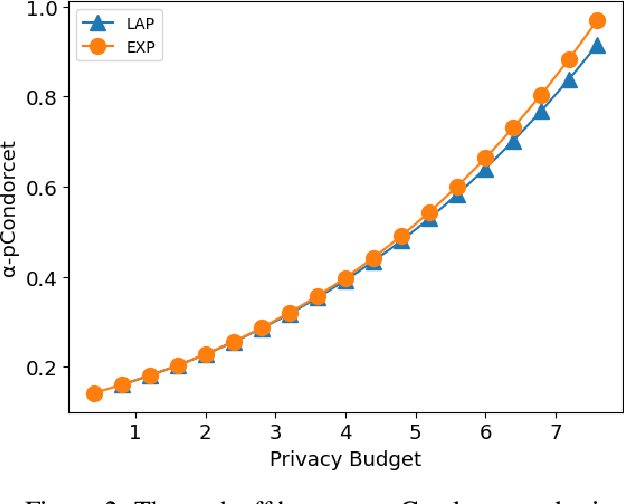
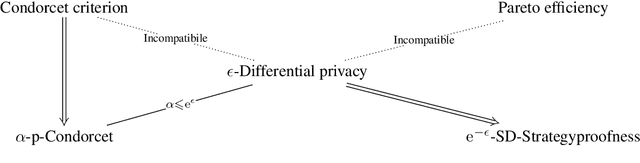
Designing private voting rules is an important and pressing problem for trustworthy democracy. In this paper, under the framework of differential privacy, we propose three classes of randomized voting rules based on the well-known Condorcet method: Laplacian Condorcet method ($CM^{LAP}_\lambda$), exponential Condorcet method ($CM^{EXP}_\lambda$), and randomized response Condorcet method ($CM^{RR}_\lambda$), where $\lambda$ represents the level of noise. By accurately estimating the errors introduced by the randomness, we show that $CM^{EXP}_\lambda$ is the most accurate mechanism in most cases. We prove that all of our rules satisfy absolute monotonicity, lexi-participation, probabilistic Pareto efficiency, approximate probabilistic Condorcet criterion, and approximate SD-strategyproofness. In addition, $CM^{RR}_\lambda$ satisfies (non-approximate) probabilistic Condorcet criterion, while $CM^{LAP}_\lambda$ and $CM^{EXP}_\lambda$ satisfy strong lexi-participation. Finally, we regard differential privacy as a voting axiom, and discuss its relations to other axioms.

Fair and Fast Tie-Breaking for Voting

We introduce a notion of fairest tie-breaking for voting w.r.t. two widely-accepted fairness criteria: anonymity (all voters being treated equally) and neutrality (all alternatives being treated equally). We proposed a polynomial-time computable fairest tie-breaking mechanism, called most-favorable-permutation (MFP) breaking, for a wide range of decision spaces, including single winners, $k$-committees, $k$-lists, and full rankings. We characterize the semi-random fairness of commonly-studied voting rules with MFP breaking, showing that it is significantly better than existing tie-breaking mechanisms, including the commonly-used lexicographic and fixed-agent mechanisms.

Anti-Malware Sandbox Games

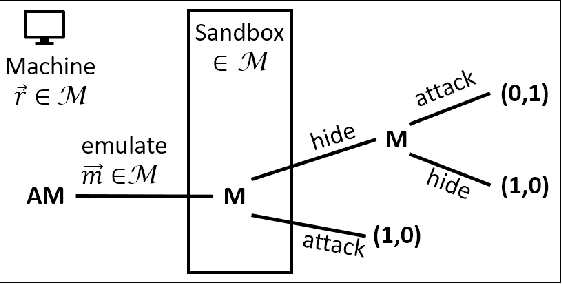
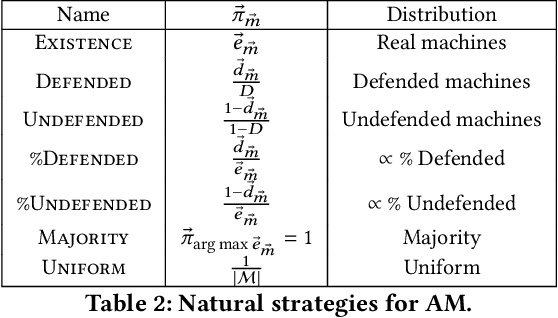
We develop a game theoretic model of malware protection using the state-of-the-art sandbox method, to characterize and compute optimal defense strategies for anti-malware. We model the strategic interaction between developers of malware (M) and anti-malware (AM) as a two player game, where AM commits to a strategy of generating sandbox environments, and M responds by choosing to either attack or hide malicious activity based on the environment it senses. We characterize the condition for AM to protect all its machines, and identify conditions under which an optimal AM strategy can be computed efficiently. For other cases, we provide a quadratically constrained quadratic program (QCQP)-based optimization framework to compute the optimal AM strategy. In addition, we identify a natural and easy to compute strategy for AM, which as we show empirically, achieves AM utility that is close to the optimal AM utility, in equilibrium.

How Likely A Coalition of Voters Can Influence A Large Election?

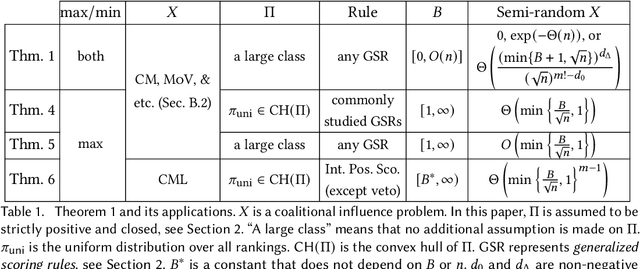
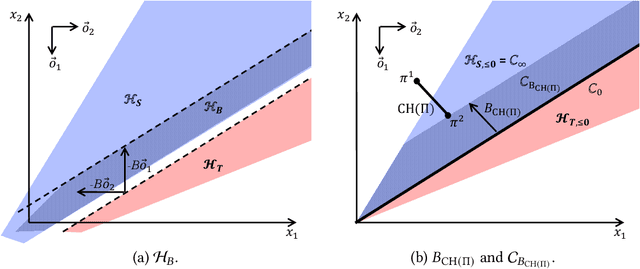
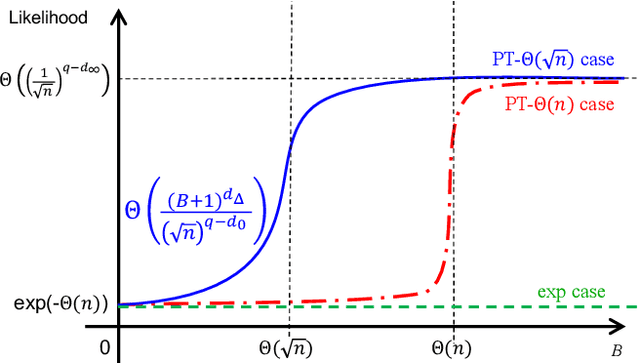
For centuries, it has been widely believed that the influence of a small coalition of voters is negligible in a large election. Consequently, there is a large body of literature on characterizing the asymptotic likelihood for an election to be influence, especially by the manipulation of a single voter, establishing an $O(\frac{1}{\sqrt n})$ upper bound and an $\Omega(\frac{1}{n^{67}})$ lower bound for many commonly studied voting rules under the i.i.d.~uniform distribution, known as Impartial Culture (IC) in social choice, where $n$ is the number is voters. In this paper, we extend previous studies in three aspects: (1) we consider a more general and realistic semi-random model that resembles the model in smoothed analysis, (2) we consider many coalitional influence problems, including coalitional manipulation, margin of victory, and various vote controls and bribery, and (3) we consider arbitrary and variable coalition size $B$. Our main theorem provides asymptotically tight bounds on the semi-random likelihood of the existence of a size-$B$ coalition that can successfully influence the election under a wide range of voting rules. Applications of the main theorem and its proof techniques resolve long-standing open questions about the likelihood of coalitional manipulability under IC, by showing that the likelihood is $\Theta\left(\min\left\{\frac{B}{\sqrt n}, 1\right\}\right)$ for many commonly studied voting rules. The main technical contribution is a characterization of the semi-random likelihood for a Poisson multinomial variable (PMV) to be unstable, which we believe to be a general and useful technique with independent interest.

Favoring Eagerness for Remaining Items: Achieving Efficient and Fair Assignments

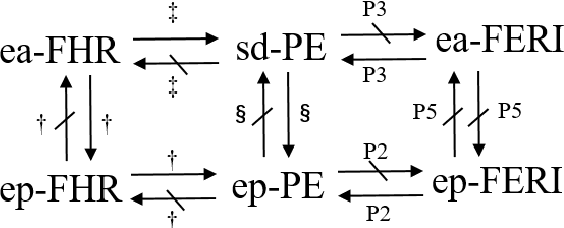
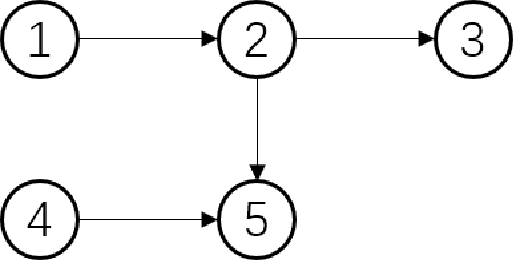
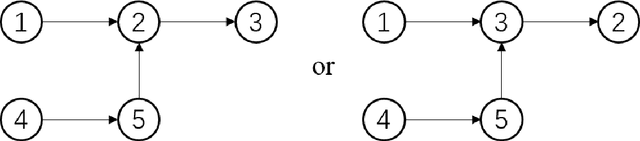
In the assignment problem, items must be assigned to agents who have unit demands, based on agents' ordinal preferences. Often the goal is to design a mechanism that is both fair and efficient. In this paper, we first prove that, unfortunately, the desirable efficiency notions rank-maximality, ex-post favoring-higher-ranks, and ex-ante favoring-higher-ranks, which aim to allocate each item to agents who rank it highest over all the items, are incompatible with the desirable fairness notions strong equal treatment of equals (SETE) and sd-weak-envy-freeness (sd-WEF) simultaneously. In light of this, we propose novel properties of efficiency based on a subtly different notion to favoring higher ranks, by favoring "eagerness" for remaining items and aiming to guarantee that each item is allocated to agents who rank it highest among remaining items. Specifically, we propose ex-post favoring-eagerness-for-remaining-items (ep-FERI) and ex-ante favoring-eagerness-for-remaining-items (ea-FERI). We prove that the eager Boston mechanism satisfies ep-FERI and sd-WSP and that the uniform probabilistic respecting eagerness mechanism satisfies ea-FERI. We also prove that both mechanisms satisfy SETE and sd-WEF, and show that no mechanism can satisfy stronger versions of envy-freeness and strategyproofness while simultaneously maintaining SETE, and either ep-FERI or ea-FERI.

Smoothed Differential Privacy

Differential privacy (DP) is a widely-accepted and widely-applied notion of privacy based on worst-case analysis. Often, DP classifies most mechanisms without external noise as non-private [Dwork et al., 2014], and external noises, such as Gaussian noise or Laplacian noise [Dwork et al., 2006], are introduced to improve privacy. In many real-world applications, however, adding external noise is undesirable and sometimes prohibited. For example, presidential elections often require a deterministic rule to be used [Liu et al., 2020], and small noises can lead to dramatic decreases in the prediction accuracy of deep neural networks, especially the underrepresented classes [Bagdasaryan et al., 2019]. In this paper, we propose a natural extension and relaxation of DP following the worst average-case idea behind the celebrated smoothed analysis [Spielman and Teng, 2004]. Our notion, the smoothed DP, can effectively measure the privacy leakage of mechanisms without external noises under realistic settings. We prove several strong properties of the smoothed DP, including composability, robustness to post-processing and etc. We proved that any discrete mechanism with sampling procedures is more private than what DP predicts. In comparison, many continuous mechanisms with sampling procedures are still non-private under smoothed DP. Experimentally, we first verified that the discrete sampling mechanisms are private in real-world elections. Then, we apply the smoothed DP notion on quantized gradient descent, which indicates some neural networks can be private without adding any extra noises. We believe that these results contribute to the theoretical foundation of realistic privacy measures beyond worst-case analysis.