Anti-Malware Sandbox Games
Paper and Code
Feb 28, 2022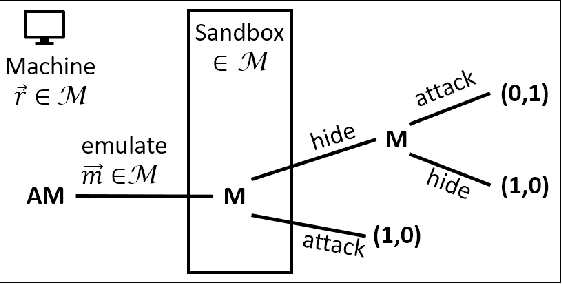


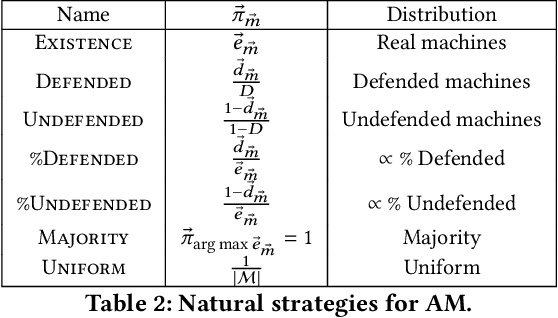
We develop a game theoretic model of malware protection using the state-of-the-art sandbox method, to characterize and compute optimal defense strategies for anti-malware. We model the strategic interaction between developers of malware (M) and anti-malware (AM) as a two player game, where AM commits to a strategy of generating sandbox environments, and M responds by choosing to either attack or hide malicious activity based on the environment it senses. We characterize the condition for AM to protect all its machines, and identify conditions under which an optimal AM strategy can be computed efficiently. For other cases, we provide a quadratically constrained quadratic program (QCQP)-based optimization framework to compute the optimal AM strategy. In addition, we identify a natural and easy to compute strategy for AM, which as we show empirically, achieves AM utility that is close to the optimal AM utility, in equilibrium.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge