Determining Winners in Elections with Absent Votes

An important question in elections is the determine whether a candidate can be a winner when some votes are absent. We study this determining winner with the absent votes (WAV) problem when the votes are top-truncated. We show that the WAV problem is NP-complete for the single transferable vote, Maximin, and Copeland, and propose a special case of positional scoring rule such that the problem can be computed in polynomial time. Our results in top-truncated rankings differ from the results in full rankings as their hardness results still hold when the number of candidates or the number of missing votes are bounded, while we show that the problem can be solved in polynomial time in either case.

Anti-Malware Sandbox Games

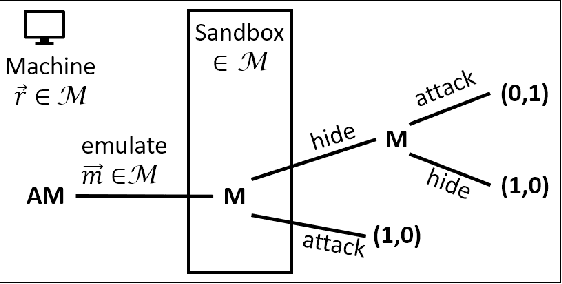
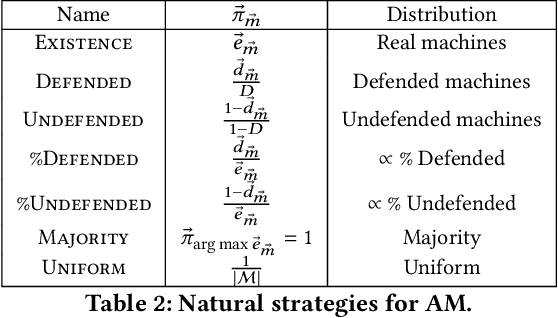
We develop a game theoretic model of malware protection using the state-of-the-art sandbox method, to characterize and compute optimal defense strategies for anti-malware. We model the strategic interaction between developers of malware (M) and anti-malware (AM) as a two player game, where AM commits to a strategy of generating sandbox environments, and M responds by choosing to either attack or hide malicious activity based on the environment it senses. We characterize the condition for AM to protect all its machines, and identify conditions under which an optimal AM strategy can be computed efficiently. For other cases, we provide a quadratically constrained quadratic program (QCQP)-based optimization framework to compute the optimal AM strategy. In addition, we identify a natural and easy to compute strategy for AM, which as we show empirically, achieves AM utility that is close to the optimal AM utility, in equilibrium.