Zhechen Li
Differentially Private Condorcet Voting
Jun 27, 2022
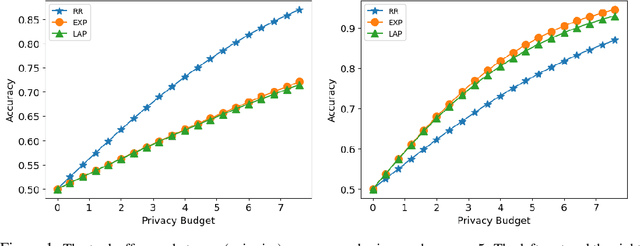
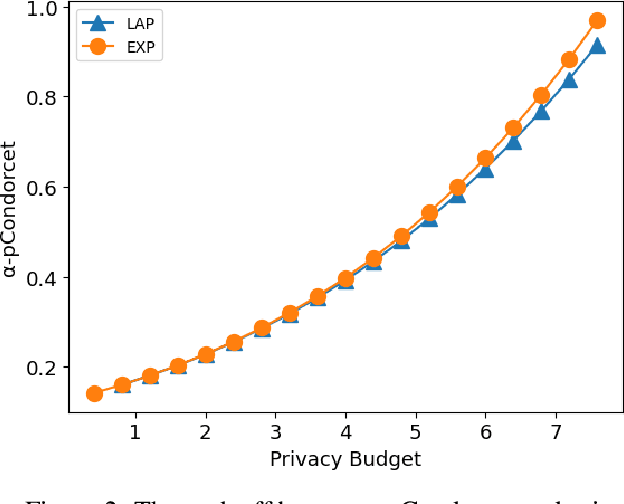
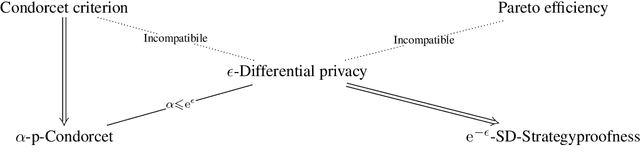
Abstract:Designing private voting rules is an important and pressing problem for trustworthy democracy. In this paper, under the framework of differential privacy, we propose three classes of randomized voting rules based on the well-known Condorcet method: Laplacian Condorcet method ($CM^{LAP}_\lambda$), exponential Condorcet method ($CM^{EXP}_\lambda$), and randomized response Condorcet method ($CM^{RR}_\lambda$), where $\lambda$ represents the level of noise. By accurately estimating the errors introduced by the randomness, we show that $CM^{EXP}_\lambda$ is the most accurate mechanism in most cases. We prove that all of our rules satisfy absolute monotonicity, lexi-participation, probabilistic Pareto efficiency, approximate probabilistic Condorcet criterion, and approximate SD-strategyproofness. In addition, $CM^{RR}_\lambda$ satisfies (non-approximate) probabilistic Condorcet criterion, while $CM^{LAP}_\lambda$ and $CM^{EXP}_\lambda$ satisfy strong lexi-participation. Finally, we regard differential privacy as a voting axiom, and discuss its relations to other axioms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge