First-Choice Maximality Meets Ex-ante and Ex-post Fairness

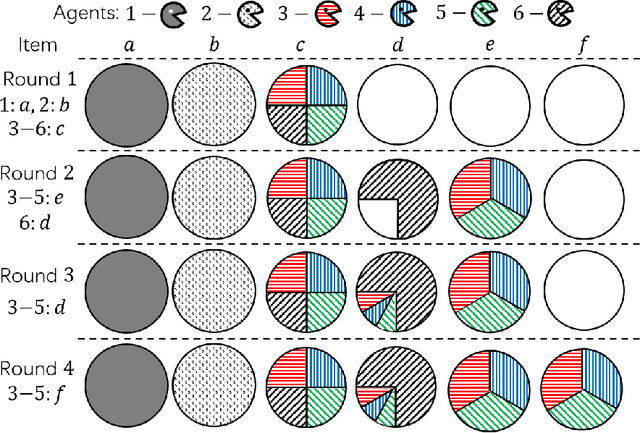
For the assignment problem where multiple indivisible items are allocated to a group of agents given their ordinal preferences, we design randomized mechanisms that satisfy first-choice maximality (FCM), i.e., maximizing the number of agents assigned their first choices, together with Pareto efficiency (PE). Our mechanisms also provide guarantees of ex-ante and ex-post fairness. The generalized eager Boston mechanism is ex-ante envy-free, and ex-post envy-free up to one item (EF1). The generalized probabilistic Boston mechanism is also ex-post EF1, and satisfies ex-ante efficiency instead of fairness. We also show that no strategyproof mechanism satisfies ex-post PE, EF1, and FCM simultaneously. In doing so, we expand the frontiers of simultaneously providing efficiency and both ex-ante and ex-post fairness guarantees for the assignment problem.

A separation logic for sequences in pointer programs and its decidability

Separation logic and its variants can describe various properties on pointer programs. However, when it comes to properties on sequences, one may find it hard to formalize. To deal with properties on variable-length sequences and multilevel data structures, we propose sequence-heap separation logic which integrates sequences into logical reasoning on heap-manipulated programs. Quantifiers over sequence variables and singleton heap storing sequence (sequence singleton heap) are new members in our logic. Further, we study the satisfiability problem of two fragments. The propositional fragment of sequence-heap separation logic is decidable, and the fragment with 2 alternations on program variables and 1 alternation on sequence variables is undecidable. In addition, we explore boundaries between decidable and undecidable fragments of the logic with prenex normal form.

Differentially Private Condorcet Voting

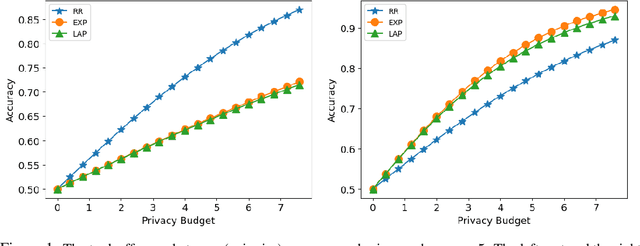
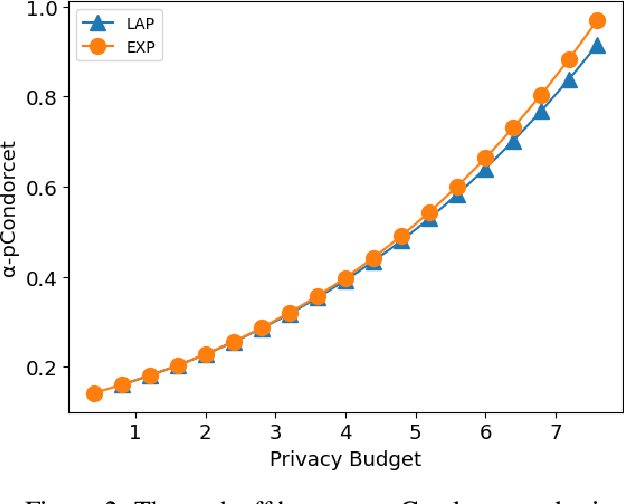
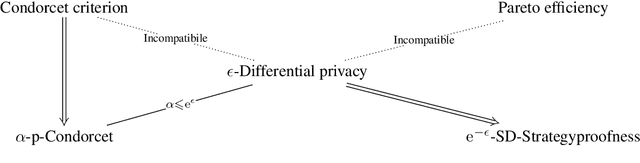
Designing private voting rules is an important and pressing problem for trustworthy democracy. In this paper, under the framework of differential privacy, we propose three classes of randomized voting rules based on the well-known Condorcet method: Laplacian Condorcet method ($CM^{LAP}_\lambda$), exponential Condorcet method ($CM^{EXP}_\lambda$), and randomized response Condorcet method ($CM^{RR}_\lambda$), where $\lambda$ represents the level of noise. By accurately estimating the errors introduced by the randomness, we show that $CM^{EXP}_\lambda$ is the most accurate mechanism in most cases. We prove that all of our rules satisfy absolute monotonicity, lexi-participation, probabilistic Pareto efficiency, approximate probabilistic Condorcet criterion, and approximate SD-strategyproofness. In addition, $CM^{RR}_\lambda$ satisfies (non-approximate) probabilistic Condorcet criterion, while $CM^{LAP}_\lambda$ and $CM^{EXP}_\lambda$ satisfy strong lexi-participation. Finally, we regard differential privacy as a voting axiom, and discuss its relations to other axioms.

Learning First-Order Rules with Differentiable Logic Program Semantics

Learning first-order logic programs (LPs) from relational facts which yields intuitive insights into the data is a challenging topic in neuro-symbolic research. We introduce a novel differentiable inductive logic programming (ILP) model, called differentiable first-order rule learner (DFOL), which finds the correct LPs from relational facts by searching for the interpretable matrix representations of LPs. These interpretable matrices are deemed as trainable tensors in neural networks (NNs). The NNs are devised according to the differentiable semantics of LPs. Specifically, we first adopt a novel propositionalization method that transfers facts to NN-readable vector pairs representing interpretation pairs. We replace the immediate consequence operator with NN constraint functions consisting of algebraic operations and a sigmoid-like activation function. We map the symbolic forward-chained format of LPs into NN constraint functions consisting of operations between subsymbolic vector representations of atoms. By applying gradient descent, the trained well parameters of NNs can be decoded into precise symbolic LPs in forward-chained logic format. We demonstrate that DFOL can perform on several standard ILP datasets, knowledge bases, and probabilistic relation facts and outperform several well-known differentiable ILP models. Experimental results indicate that DFOL is a precise, robust, scalable, and computationally cheap differentiable ILP model.

Favoring Eagerness for Remaining Items: Achieving Efficient and Fair Assignments

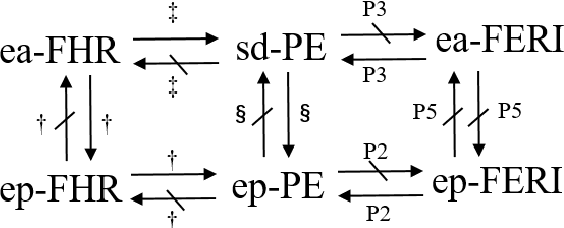
In the assignment problem, items must be assigned to agents who have unit demands, based on agents' ordinal preferences. Often the goal is to design a mechanism that is both fair and efficient. In this paper, we first prove that, unfortunately, the desirable efficiency notions rank-maximality, ex-post favoring-higher-ranks, and ex-ante favoring-higher-ranks, which aim to allocate each item to agents who rank it highest over all the items, are incompatible with the desirable fairness notions strong equal treatment of equals (SETE) and sd-weak-envy-freeness (sd-WEF) simultaneously. In light of this, we propose novel properties of efficiency based on a subtly different notion to favoring higher ranks, by favoring "eagerness" for remaining items and aiming to guarantee that each item is allocated to agents who rank it highest among remaining items. Specifically, we propose ex-post favoring-eagerness-for-remaining-items (ep-FERI) and ex-ante favoring-eagerness-for-remaining-items (ea-FERI). We prove that the eager Boston mechanism satisfies ep-FERI and sd-WSP and that the uniform probabilistic respecting eagerness mechanism satisfies ea-FERI. We also prove that both mechanisms satisfy SETE and sd-WEF, and show that no mechanism can satisfy stronger versions of envy-freeness and strategyproofness while simultaneously maintaining SETE, and either ep-FERI or ea-FERI.

Sequential Mechanisms for Multi-type Resource Allocation

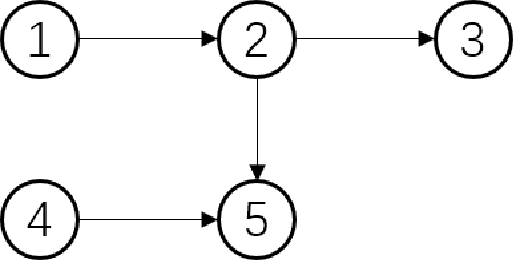
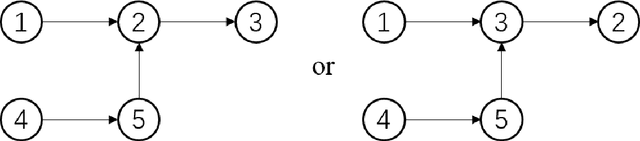
Several resource allocation problems involve multiple types of resources, with a different agency being responsible for "locally" allocating the resources of each type, while a central planner wishes to provide a guarantee on the properties of the final allocation given agents' preferences. We study the relationship between properties of the local mechanisms, each responsible for assigning all of the resources of a designated type, and the properties of a sequential mechanism which is composed of these local mechanisms, one for each type, applied sequentially, under lexicographic preferences, a well studied model of preferences over multiple types of resources in artificial intelligence and economics. We show that when preferences are O-legal, meaning that agents share a common importance order on the types, sequential mechanisms satisfy the desirable properties of anonymity, neutrality, non-bossiness, or Pareto-optimality if and only if every local mechanism also satisfies the same property, and they are applied sequentially according to the order O. Our main results are that under O-legal lexicographic preferences, every mechanism satisfying strategyproofness and a combination of these properties must be a sequential composition of local mechanisms that are also strategyproof, and satisfy the same combinations of properties.

Probabilistic Serial Mechanism for Multi-Type Resource Allocation

In multi-type resource allocation (MTRA) problems, there are p $\ge$ 2 types of items, and n agents, who each demand one unit of items of each type, and have strict linear preferences over bundles consisting of one item of each type. For MTRAs with indivisible items, our first result is an impossibility theorem that is in direct contrast to the single type (p = 1) setting: No mechanism, the output of which is always decomposable into a probability distribution over discrete assignments (where no item is split between agents), can satisfy both sd-efficiency and sd-envy-freeness. To circumvent this impossibility result, we consider the natural assumption of lexicographic preference, and provide an extension of the probabilistic serial (PS), called lexicographic probabilistic serial (LexiPS).We prove that LexiPS satisfies sd-efficiency and sd-envy-freeness, retaining the desirable properties of PS. Moreover, LexiPS satisfies sd-weak-strategyproofness when agents are not allowed to misreport their importance orders. For MTRAs with divisible items, we show that the existing multi-type probabilistic serial (MPS) mechanism satisfies the stronger efficiency notion of lexi-efficiency, and is sd-envy-free under strict linear preferences, and sd-weak-strategyproof under lexicographic preferences. We also prove that MPS can be characterized both by leximin-ptimality and by item-wise ordinal fairness, and the family of eating algorithms which MPS belongs to can be characterized by no-generalized-cycle condition.

Multi-type Resource Allocation with Partial Preferences

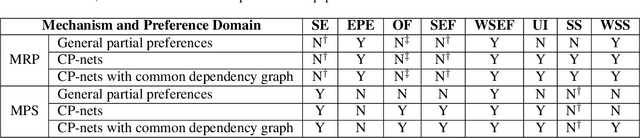
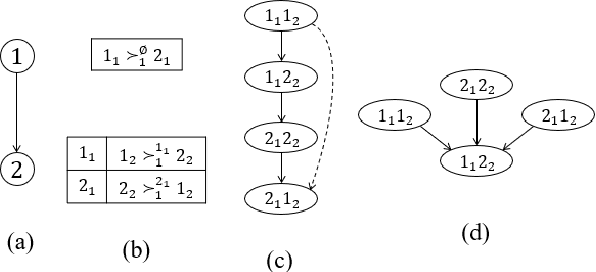
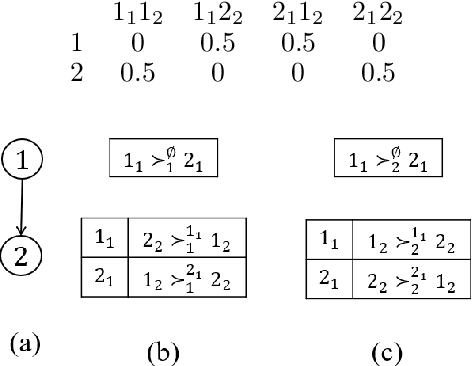
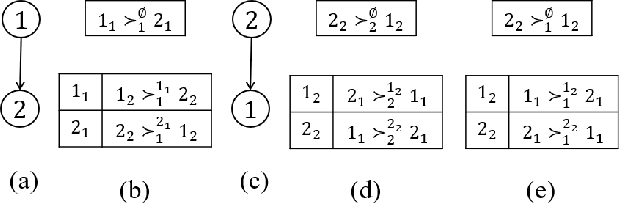
We propose multi-type probabilistic serial (MPS) and multi-type random priority (MRP) as extensions of the well known PS and RP mechanisms to the multi-type resource allocation problem (MTRA) with partial preferences. In our setting, there are multiple types of divisible items, and a group of agents who have partial order preferences over bundles consisting of one item of each type. We show that for the unrestricted domain of partial order preferences, no mechanism satisfies both sd-efficiency and sd-envy-freeness. Notwithstanding this impossibility result, our main message is positive: When agents' preferences are represented by acyclic CP-nets, MPS satisfies sd-efficiency, sd-envy-freeness, ordinal fairness, and upper invariance, while MRP satisfies ex-post-efficiency, sd-strategy-proofness, and upper invariance, recovering the properties of PS and RP.

A Behavioral Distance for Fuzzy-Transition Systems

In contrast to the existing approaches to bisimulation for fuzzy systems, we introduce a behavioral distance to measure the behavioral similarity of states in a nondeterministic fuzzy-transition system. This behavioral distance is defined as the greatest fixed point of a suitable monotonic function and provides a quantitative analogue of bisimilarity. The behavioral distance has the important property that two states are at zero distance if and only if they are bisimilar. Moreover, for any given threshold, we find that states with behavioral distances bounded by the threshold are equivalent. In addition, we show that two system combinators---parallel composition and product---are non-expansive with respect to our behavioral distance, which makes compositional verification possible.

Nondeterministic fuzzy automata

Fuzzy automata have long been accepted as a generalization of nondeterministic finite automata. A closer examination, however, shows that the fundamental property---nondeterminism---in nondeterministic finite automata has not been well embodied in the generalization. In this paper, we introduce nondeterministic fuzzy automata with or without $\el$-moves and fuzzy languages recognized by them. Furthermore, we prove that (deterministic) fuzzy automata, nondeterministic fuzzy automata, and nondeterministic fuzzy automata with $\el$-moves are all equivalent in the sense that they recognize the same class of fuzzy languages.