Multi-type Resource Allocation with Partial Preferences
Paper and Code
Jun 13, 2019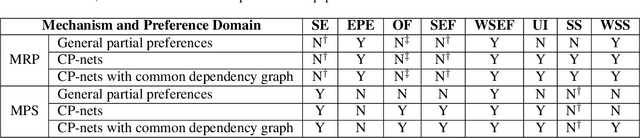
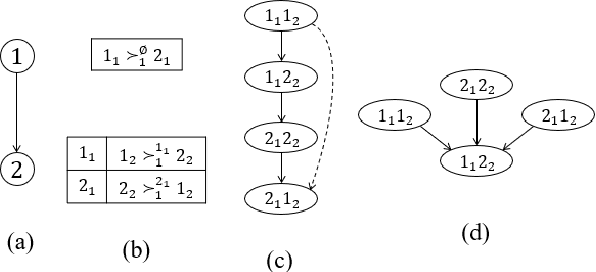
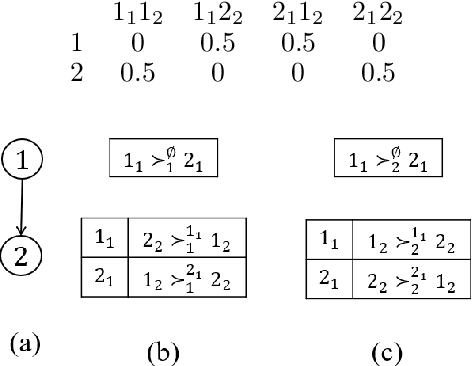
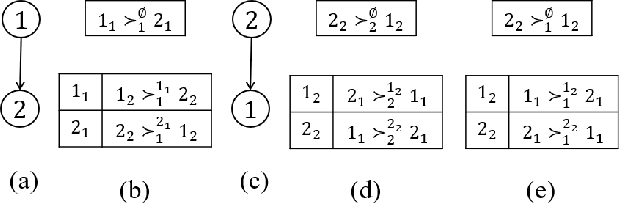
We propose multi-type probabilistic serial (MPS) and multi-type random priority (MRP) as extensions of the well known PS and RP mechanisms to the multi-type resource allocation problem (MTRA) with partial preferences. In our setting, there are multiple types of divisible items, and a group of agents who have partial order preferences over bundles consisting of one item of each type. We show that for the unrestricted domain of partial order preferences, no mechanism satisfies both sd-efficiency and sd-envy-freeness. Notwithstanding this impossibility result, our main message is positive: When agents' preferences are represented by acyclic CP-nets, MPS satisfies sd-efficiency, sd-envy-freeness, ordinal fairness, and upper invariance, while MRP satisfies ex-post-efficiency, sd-strategy-proofness, and upper invariance, recovering the properties of PS and RP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge