First-Choice Maximality Meets Ex-ante and Ex-post Fairness

For the assignment problem where multiple indivisible items are allocated to a group of agents given their ordinal preferences, we design randomized mechanisms that satisfy first-choice maximality (FCM), i.e., maximizing the number of agents assigned their first choices, together with Pareto efficiency (PE). Our mechanisms also provide guarantees of ex-ante and ex-post fairness. The generalized eager Boston mechanism is ex-ante envy-free, and ex-post envy-free up to one item (EF1). The generalized probabilistic Boston mechanism is also ex-post EF1, and satisfies ex-ante efficiency instead of fairness. We also show that no strategyproof mechanism satisfies ex-post PE, EF1, and FCM simultaneously. In doing so, we expand the frontiers of simultaneously providing efficiency and both ex-ante and ex-post fairness guarantees for the assignment problem.

Favoring Eagerness for Remaining Items: Achieving Efficient and Fair Assignments

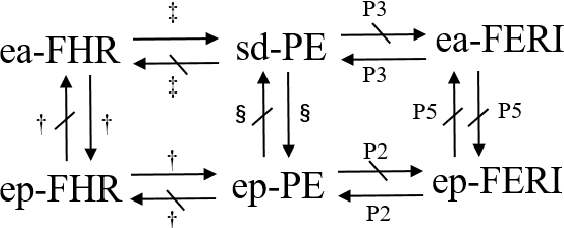
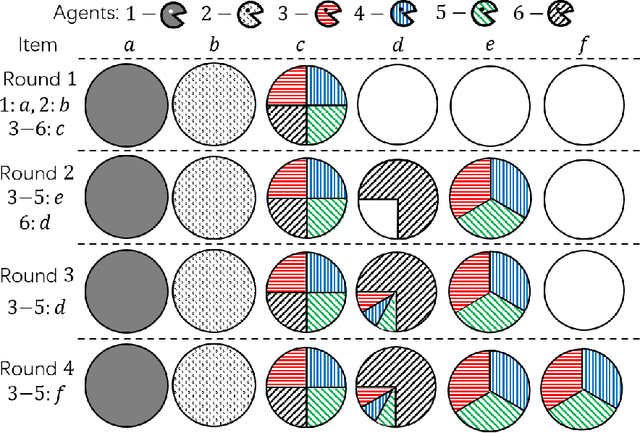
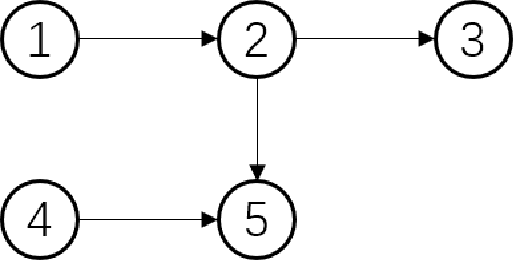
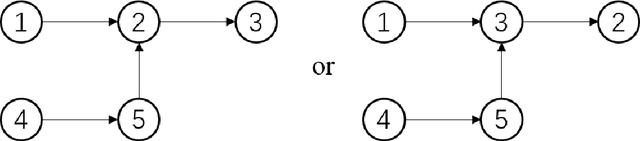
In the assignment problem, items must be assigned to agents who have unit demands, based on agents' ordinal preferences. Often the goal is to design a mechanism that is both fair and efficient. In this paper, we first prove that, unfortunately, the desirable efficiency notions rank-maximality, ex-post favoring-higher-ranks, and ex-ante favoring-higher-ranks, which aim to allocate each item to agents who rank it highest over all the items, are incompatible with the desirable fairness notions strong equal treatment of equals (SETE) and sd-weak-envy-freeness (sd-WEF) simultaneously. In light of this, we propose novel properties of efficiency based on a subtly different notion to favoring higher ranks, by favoring "eagerness" for remaining items and aiming to guarantee that each item is allocated to agents who rank it highest among remaining items. Specifically, we propose ex-post favoring-eagerness-for-remaining-items (ep-FERI) and ex-ante favoring-eagerness-for-remaining-items (ea-FERI). We prove that the eager Boston mechanism satisfies ep-FERI and sd-WSP and that the uniform probabilistic respecting eagerness mechanism satisfies ea-FERI. We also prove that both mechanisms satisfy SETE and sd-WEF, and show that no mechanism can satisfy stronger versions of envy-freeness and strategyproofness while simultaneously maintaining SETE, and either ep-FERI or ea-FERI.

Sequential Mechanisms for Multi-type Resource Allocation

Several resource allocation problems involve multiple types of resources, with a different agency being responsible for "locally" allocating the resources of each type, while a central planner wishes to provide a guarantee on the properties of the final allocation given agents' preferences. We study the relationship between properties of the local mechanisms, each responsible for assigning all of the resources of a designated type, and the properties of a sequential mechanism which is composed of these local mechanisms, one for each type, applied sequentially, under lexicographic preferences, a well studied model of preferences over multiple types of resources in artificial intelligence and economics. We show that when preferences are O-legal, meaning that agents share a common importance order on the types, sequential mechanisms satisfy the desirable properties of anonymity, neutrality, non-bossiness, or Pareto-optimality if and only if every local mechanism also satisfies the same property, and they are applied sequentially according to the order O. Our main results are that under O-legal lexicographic preferences, every mechanism satisfying strategyproofness and a combination of these properties must be a sequential composition of local mechanisms that are also strategyproof, and satisfy the same combinations of properties.

Probabilistic Serial Mechanism for Multi-Type Resource Allocation

In multi-type resource allocation (MTRA) problems, there are p $\ge$ 2 types of items, and n agents, who each demand one unit of items of each type, and have strict linear preferences over bundles consisting of one item of each type. For MTRAs with indivisible items, our first result is an impossibility theorem that is in direct contrast to the single type (p = 1) setting: No mechanism, the output of which is always decomposable into a probability distribution over discrete assignments (where no item is split between agents), can satisfy both sd-efficiency and sd-envy-freeness. To circumvent this impossibility result, we consider the natural assumption of lexicographic preference, and provide an extension of the probabilistic serial (PS), called lexicographic probabilistic serial (LexiPS).We prove that LexiPS satisfies sd-efficiency and sd-envy-freeness, retaining the desirable properties of PS. Moreover, LexiPS satisfies sd-weak-strategyproofness when agents are not allowed to misreport their importance orders. For MTRAs with divisible items, we show that the existing multi-type probabilistic serial (MPS) mechanism satisfies the stronger efficiency notion of lexi-efficiency, and is sd-envy-free under strict linear preferences, and sd-weak-strategyproof under lexicographic preferences. We also prove that MPS can be characterized both by leximin-ptimality and by item-wise ordinal fairness, and the family of eating algorithms which MPS belongs to can be characterized by no-generalized-cycle condition.

Multi-type Resource Allocation with Partial Preferences

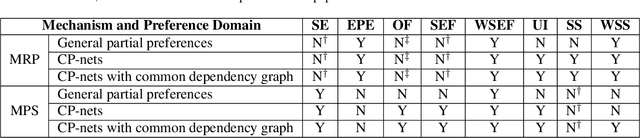
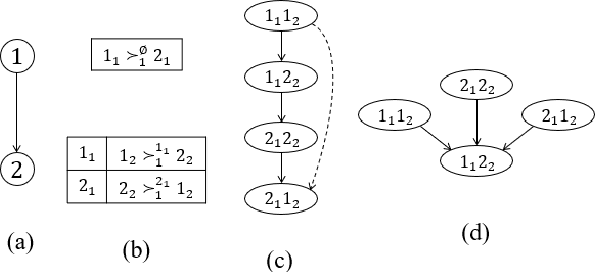
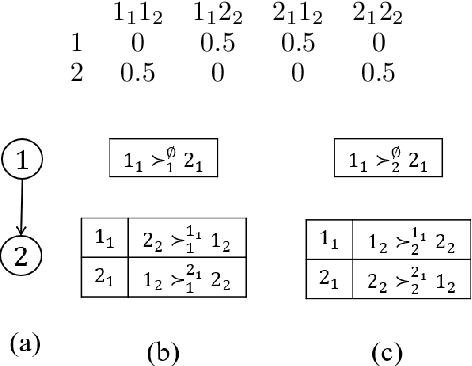
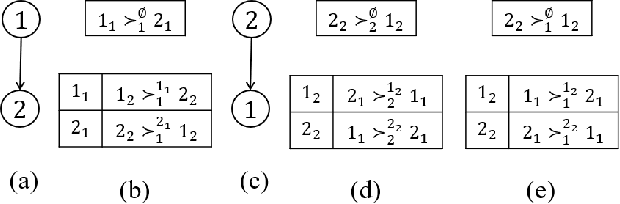
We propose multi-type probabilistic serial (MPS) and multi-type random priority (MRP) as extensions of the well known PS and RP mechanisms to the multi-type resource allocation problem (MTRA) with partial preferences. In our setting, there are multiple types of divisible items, and a group of agents who have partial order preferences over bundles consisting of one item of each type. We show that for the unrestricted domain of partial order preferences, no mechanism satisfies both sd-efficiency and sd-envy-freeness. Notwithstanding this impossibility result, our main message is positive: When agents' preferences are represented by acyclic CP-nets, MPS satisfies sd-efficiency, sd-envy-freeness, ordinal fairness, and upper invariance, while MRP satisfies ex-post-efficiency, sd-strategy-proofness, and upper invariance, recovering the properties of PS and RP.