Favoring Eagerness for Remaining Items: Achieving Efficient and Fair Assignments

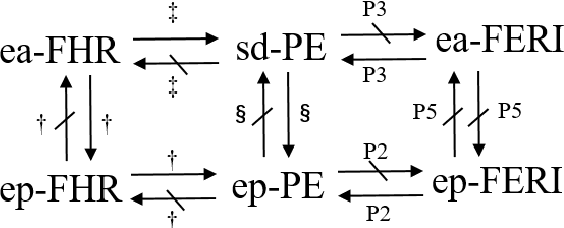
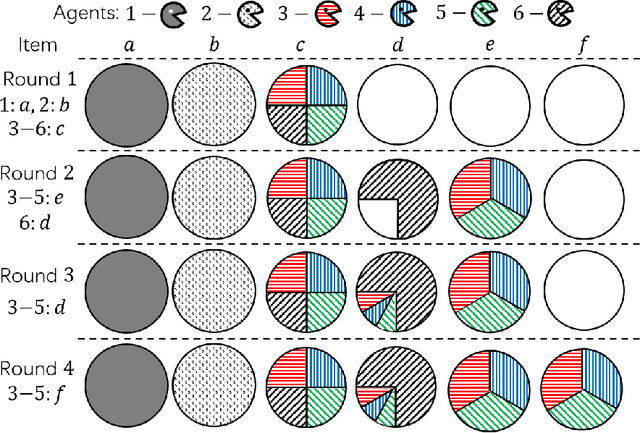
In the assignment problem, items must be assigned to agents who have unit demands, based on agents' ordinal preferences. Often the goal is to design a mechanism that is both fair and efficient. In this paper, we first prove that, unfortunately, the desirable efficiency notions rank-maximality, ex-post favoring-higher-ranks, and ex-ante favoring-higher-ranks, which aim to allocate each item to agents who rank it highest over all the items, are incompatible with the desirable fairness notions strong equal treatment of equals (SETE) and sd-weak-envy-freeness (sd-WEF) simultaneously. In light of this, we propose novel properties of efficiency based on a subtly different notion to favoring higher ranks, by favoring "eagerness" for remaining items and aiming to guarantee that each item is allocated to agents who rank it highest among remaining items. Specifically, we propose ex-post favoring-eagerness-for-remaining-items (ep-FERI) and ex-ante favoring-eagerness-for-remaining-items (ea-FERI). We prove that the eager Boston mechanism satisfies ep-FERI and sd-WSP and that the uniform probabilistic respecting eagerness mechanism satisfies ea-FERI. We also prove that both mechanisms satisfy SETE and sd-WEF, and show that no mechanism can satisfy stronger versions of envy-freeness and strategyproofness while simultaneously maintaining SETE, and either ep-FERI or ea-FERI.