Neural Logic Networks for Interpretable Classification

Traditional neural networks have an impressive classification performance, but what they learn cannot be inspected, verified or extracted. Neural Logic Networks on the other hand have an interpretable structure that enables them to learn a logical mechanism relating the inputs and outputs with AND and OR operations. We generalize these networks with NOT operations and biases that take into account unobserved data and develop a rigorous logical and probabilistic modeling in terms of concept combinations to motivate their use. We also propose a novel factorized IF-THEN rule structure for the model as well as a modified learning algorithm. Our method improves the state-of-the-art in Boolean networks discovery and is able to learn relevant, interpretable rules in tabular classification, notably on an example from the medical field where interpretability has tangible value.

A Rule-Based Approach to Specifying Preferences over Conflicting Facts and Querying Inconsistent Knowledge Bases

Repair-based semantics have been extensively studied as a means of obtaining meaningful answers to queries posed over inconsistent knowledge bases (KBs). While several works have considered how to exploit a priority relation between facts to select optimal repairs, the question of how to specify such preferences remains largely unaddressed. This motivates us to introduce a declarative rule-based framework for specifying and computing a priority relation between conflicting facts. As the expressed preferences may contain undesirable cycles, we consider the problem of determining when a set of preference rules always yields an acyclic relation, and we also explore a pragmatic approach that extracts an acyclic relation by applying various cycle removal techniques. Towards an end-to-end system for querying inconsistent KBs, we present a preliminary implementation and experimental evaluation of the framework, which employs answer set programming to evaluate the preference rules, apply the desired cycle resolution techniques to obtain a priority relation, and answer queries under prioritized-repair semantics.

Neuro-Symbolic Contrastive Learning for Cross-domain Inference

Pre-trained language models (PLMs) have made significant advances in natural language inference (NLI) tasks, however their sensitivity to textual perturbations and dependence on large datasets indicate an over-reliance on shallow heuristics. In contrast, inductive logic programming (ILP) excels at inferring logical relationships across diverse, sparse and limited datasets, but its discrete nature requires the inputs to be precisely specified, which limits their application. This paper proposes a bridge between the two approaches: neuro-symbolic contrastive learning. This allows for smooth and differentiable optimisation that improves logical accuracy across an otherwise discrete, noisy, and sparse topological space of logical functions. We show that abstract logical relationships can be effectively embedded within a neuro-symbolic paradigm, by representing data as logic programs and sets of logic rules. The embedding space captures highly varied textual information with similar semantic logical relations, but can also separate similar textual relations that have dissimilar logical relations. Experimental results demonstrate that our approach significantly improves the inference capabilities of the models in terms of generalisation and reasoning.

Transformers Use Causal World Models in Maze-Solving Tasks

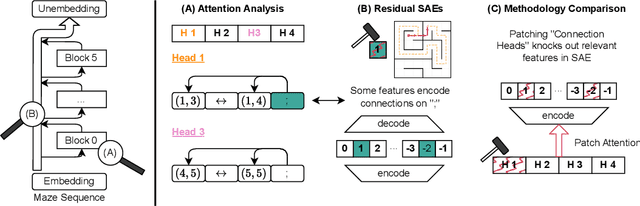
Recent studies in interpretability have explored the inner workings of transformer models trained on tasks across various domains, often discovering that these networks naturally develop surprisingly structured representations. When such representations comprehensively reflect the task domain's structure, they are commonly referred to as ``World Models'' (WMs). In this work, we discover such WMs in transformers trained on maze tasks. In particular, by employing Sparse Autoencoders (SAEs) and analysing attention patterns, we examine the construction of WMs and demonstrate consistency between the circuit analysis and the SAE feature-based analysis. We intervene upon the isolated features to confirm their causal role and, in doing so, find asymmetries between certain types of interventions. Surprisingly, we find that models are able to reason with respect to a greater number of active features than they see during training, even if attempting to specify these in the input token sequence would lead the model to fail. Futhermore, we observe that varying positional encodings can alter how WMs are encoded in a model's residual stream. By analyzing the causal role of these WMs in a toy domain we hope to make progress toward an understanding of emergent structure in the representations acquired by Transformers, leading to the development of more interpretable and controllable AI systems.

Generating Global and Local Explanations for Tree-Ensemble Learning Methods by Answer Set Programming

We propose a method for generating rule sets as global and local explanations for tree-ensemble learning methods using Answer Set Programming (ASP). To this end, we adopt a decompositional approach where the split structures of the base decision trees are exploited in the construction of rules, which in turn are assessed using pattern mining methods encoded in ASP to extract explanatory rules. For global explanations, candidate rules are chosen from the entire trained tree-ensemble models, whereas for local explanations, candidate rules are selected by only considering rules that are relevant to the particular predicted instance. We show how user-defined constraints and preferences can be represented declaratively in ASP to allow for transparent and flexible rule set generation, and how rules can be used as explanations to help the user better understand the models. Experimental evaluation with real-world datasets and popular tree-ensemble algorithms demonstrates that our approach is applicable to a wide range of classification tasks. Under consideration in Theory and Practice of Logic Programming (TPLP).

Differentiable Logic Programming for Distant Supervision

We introduce a new method for integrating neural networks with logic programming in Neural-Symbolic AI (NeSy), aimed at learning with distant supervision, in which direct labels are unavailable. Unlike prior methods, our approach does not depend on symbolic solvers for reasoning about missing labels. Instead, it evaluates logical implications and constraints in a differentiable manner by embedding both neural network outputs and logic programs into matrices. This method facilitates more efficient learning under distant supervision. We evaluated our approach against existing methods while maintaining a constant volume of training data. The findings indicate that our method not only matches or exceeds the accuracy of other methods across various tasks but also speeds up the learning process. These results highlight the potential of our approach to enhance both accuracy and learning efficiency in NeSy applications.

Variable Assignment Invariant Neural Networks for Learning Logic Programs

Learning from interpretation transition (LFIT) is a framework for learning rules from observed state transitions. LFIT has been implemented in purely symbolic algorithms, but they are unable to deal with noise or generalize to unobserved transitions. Rule extraction based neural network methods suffer from overfitting, while more general implementation that categorize rules suffer from combinatorial explosion. In this paper, we introduce a technique to leverage variable permutation invariance inherent in symbolic domains. Our technique ensures that the permutation and the naming of the variables would not affect the results. We demonstrate the effectiveness and the scalability of this method with various experiments. Our code is publicly available at https://github.com/phuayj/delta-lfit-2

Abductive Reasoning in a Paraconsistent Framework

We explore the problem of explaining observations starting from a classically inconsistent theory by adopting a paraconsistent framework. We consider two expansions of the well-known Belnap--Dunn paraconsistent four-valued logic $\mathsf{BD}$: $\mathsf{BD}_\circ$ introduces formulas of the form $\circ\phi$ (the information on $\phi$ is reliable), while $\mathsf{BD}_\triangle$ augments the language with $\triangle\phi$'s (there is information that $\phi$ is true). We define and motivate the notions of abduction problems and explanations in $\mathsf{BD}_\circ$ and $\mathsf{BD}_\triangle$ and show that they are not reducible to one another. We analyse the complexity of standard abductive reasoning tasks (solution recognition, solution existence, and relevance / necessity of hypotheses) in both logics. Finally, we show how to reduce abduction in $\mathsf{BD}_\circ$ and $\mathsf{BD}_\triangle$ to abduction in classical propositional logic, thereby enabling the reuse of existing abductive reasoning procedures.

Large Neighborhood Prioritized Search for Combinatorial Optimization with Answer Set Programming

We propose Large Neighborhood Prioritized Search (LNPS) for solving combinatorial optimization problems in Answer Set Programming (ASP). LNPS is a metaheuristic that starts with an initial solution and then iteratively tries to find better solutions by alternately destroying and prioritized searching for a current solution. Due to the variability of neighborhoods, LNPS allows for flexible search without strongly depending on the destroy operators. We present an implementation of LNPS based on ASP. The resulting heulingo solver demonstrates that LNPS can significantly enhance the solving performance of ASP for optimization. Furthermore, we establish the competitiveness of our LNPS approach by empirically contrasting it to (adaptive) large neighborhood search.

Structured World Representations in Maze-Solving Transformers

Transformer models underpin many recent advances in practical machine learning applications, yet understanding their internal behavior continues to elude researchers. Given the size and complexity of these models, forming a comprehensive picture of their inner workings remains a significant challenge. To this end, we set out to understand small transformer models in a more tractable setting: that of solving mazes. In this work, we focus on the abstractions formed by these models and find evidence for the consistent emergence of structured internal representations of maze topology and valid paths. We demonstrate this by showing that the residual stream of only a single token can be linearly decoded to faithfully reconstruct the entire maze. We also find that the learned embeddings of individual tokens have spatial structure. Furthermore, we take steps towards deciphering the circuity of path-following by identifying attention heads (dubbed $\textit{adjacency heads}$), which are implicated in finding valid subsequent tokens.