Dominating Set Reconfiguration with Answer Set Programming

The dominating set reconfiguration problem is defined as determining, for a given dominating set problem and two among its feasible solutions, whether one is reachable from the other via a sequence of feasible solutions subject to a certain adjacency relation. This problem is PSPACE-complete in general. The concept of the dominating set is known to be quite useful for analyzing wireless networks, social networks, and sensor networks. We develop an approach to solve the dominating set reconfiguration problem based on Answer Set Programming (ASP). Our declarative approach relies on a high-level ASP encoding, and both the grounding and solving tasks are delegated to an ASP-based combinatorial reconfiguration solver. To evaluate the effectiveness of our approach, we conduct experiments on a newly created benchmark set.

Large Neighborhood Prioritized Search for Combinatorial Optimization with Answer Set Programming

We propose Large Neighborhood Prioritized Search (LNPS) for solving combinatorial optimization problems in Answer Set Programming (ASP). LNPS is a metaheuristic that starts with an initial solution and then iteratively tries to find better solutions by alternately destroying and prioritized searching for a current solution. Due to the variability of neighborhoods, LNPS allows for flexible search without strongly depending on the destroy operators. We present an implementation of LNPS based on ASP. The resulting heulingo solver demonstrates that LNPS can significantly enhance the solving performance of ASP for optimization. Furthermore, we establish the competitiveness of our LNPS approach by empirically contrasting it to (adaptive) large neighborhood search.

Bounded Combinatorial Reconfiguration with Answer Set Programming

We develop an approach called bounded combinatorial reconfiguration for solving combinatorial reconfiguration problems based on Answer Set Programming (ASP). The general task is to study the solution spaces of source combinatorial problems and to decide whether or not there are sequences of feasible solutions that have special properties. The resulting recongo solver covers all metrics of the solver track in the most recent international competition on combinatorial reconfiguration (CoRe Challenge 2022). recongo ranked first in the shortest metric of the single-engine solvers track. In this paper, we present the design and implementation of bounded combinatorial reconfiguration, and present an ASP encoding of the independent set reconfiguration problem that is one of the most studied combinatorial reconfiguration problems. Finally, we present empirical analysis considering all instances of CoRe Challenge 2022.

Clingcon: The Next Generation

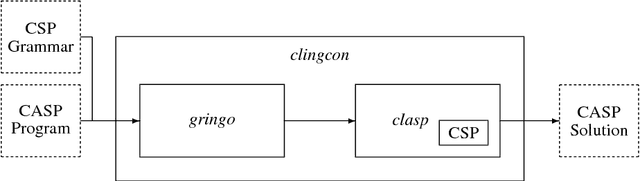
We present the third generation of the constraint answer set system clingcon, combining Answer Set Programming (ASP) with finite domain constraint processing (CP). While its predecessors rely on a black-box approach to hybrid solving by integrating the CP solver gecode, the new clingcon system pursues a lazy approach using dedicated constraint propagators to extend propagation in the underlying ASP solver clasp. No extension is needed for parsing and grounding clingcon's hybrid modeling language since both can be accommodated by the new generic theory handling capabilities of the ASP grounder gringo. As a whole, clingcon 3 is thus an extension of the ASP system clingo 5, which itself relies on the grounder gringo and the solver clasp. The new approach of clingcon offers a seamless integration of CP propagation into ASP solving that benefits from the whole spectrum of clasp's reasoning modes, including for instance multi-shot solving and advanced optimization techniques. This is accomplished by a lazy approach that unfolds the representation of constraints and adds it to that of the logic program only when needed. Although the unfolding is usually dictated by the constraint propagators during solving, it can already be partially (or even totally) done during preprocessing. Moreover, clingcon's constraint preprocessing and propagation incorporate several well established CP techniques that greatly improve its performance. We demonstrate this via an extensive empirical evaluation contrasting, first, the various techniques in the context of CSP solving and, second, the new clingcon system with other hybrid ASP systems. Under consideration in Theory and Practice of Logic Programming (TPLP)

Aspartame: Solving Constraint Satisfaction Problems with Answer Set Programming

Encoding finite linear CSPs as Boolean formulas and solving them by using modern SAT solvers has proven to be highly effective, as exemplified by the award-winning sugar system. We here develop an alternative approach based on ASP. This allows us to use first-order encodings providing us with a high degree of flexibility for easy experimentation with different implementations. The resulting system aspartame re-uses parts of sugar for parsing and normalizing CSPs. The obtained set of facts is then combined with an ASP encoding that can be grounded and solved by off-the-shelf ASP systems. We establish the competitiveness of our approach by empirically contrasting aspartame and sugar.