Structured World Representations in Maze-Solving Transformers
Paper and Code
Dec 05, 2023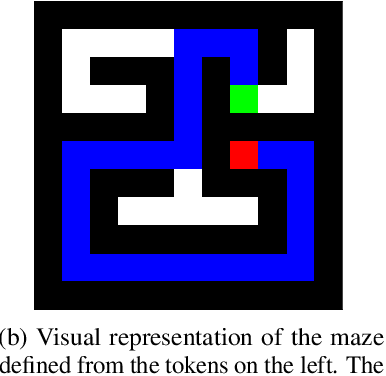
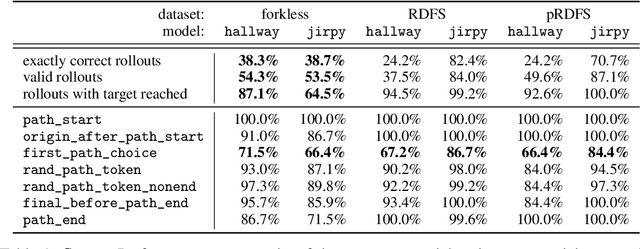
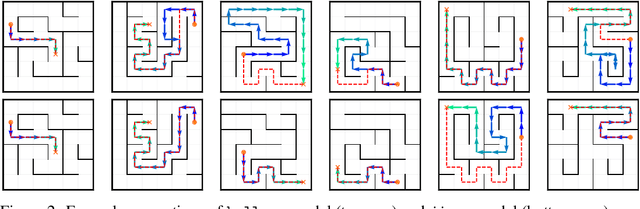

Transformer models underpin many recent advances in practical machine learning applications, yet understanding their internal behavior continues to elude researchers. Given the size and complexity of these models, forming a comprehensive picture of their inner workings remains a significant challenge. To this end, we set out to understand small transformer models in a more tractable setting: that of solving mazes. In this work, we focus on the abstractions formed by these models and find evidence for the consistent emergence of structured internal representations of maze topology and valid paths. We demonstrate this by showing that the residual stream of only a single token can be linearly decoded to faithfully reconstruct the entire maze. We also find that the learned embeddings of individual tokens have spatial structure. Furthermore, we take steps towards deciphering the circuity of path-following by identifying attention heads (dubbed $\textit{adjacency heads}$), which are implicated in finding valid subsequent tokens.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge