Slowing Learning by Erasing Simple Features

Prior work suggests that neural networks tend to learn low-order moments of the data distribution first, before moving on to higher-order correlations. In this work, we derive a novel closed-form concept erasure method, QLEACE, which surgically removes all quadratically available information about a concept from a representation. Through comparisons with linear erasure (LEACE) and two approximate forms of quadratic erasure, we explore whether networks can still learn when low-order statistics are removed from image classification datasets. We find that while LEACE consistently slows learning, quadratic erasure can exhibit both positive and negative effects on learning speed depending on the choice of dataset, model architecture, and erasure method. Use of QLEACE consistently slows learning in feedforward architectures, but more sophisticated architectures learn to use injected higher order Shannon information about class labels. Its approximate variants avoid injecting information, but surprisingly act as data augmentation techniques on some datasets, enhancing learning speed compared to LEACE.

Neural Networks Learn Statistics of Increasing Complexity

The distributional simplicity bias (DSB) posits that neural networks learn low-order moments of the data distribution first, before moving on to higher-order correlations. In this work, we present compelling new evidence for the DSB by showing that networks automatically learn to perform well on maximum-entropy distributions whose low-order statistics match those of the training set early in training, then lose this ability later. We also extend the DSB to discrete domains by proving an equivalence between token $n$-gram frequencies and the moments of embedding vectors, and by finding empirical evidence for the bias in LLMs. Finally we use optimal transport methods to surgically edit the low-order statistics of one class to match those of another, and show that early-training networks treat the edited samples as if they were drawn from the target class. Code is available at https://github.com/EleutherAI/features-across-time.

Structured World Representations in Maze-Solving Transformers

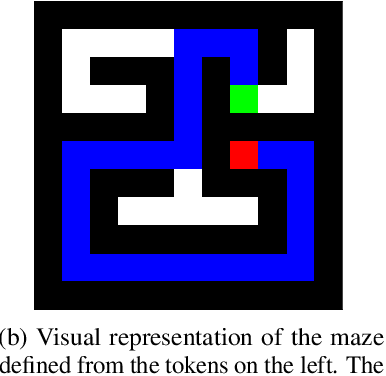
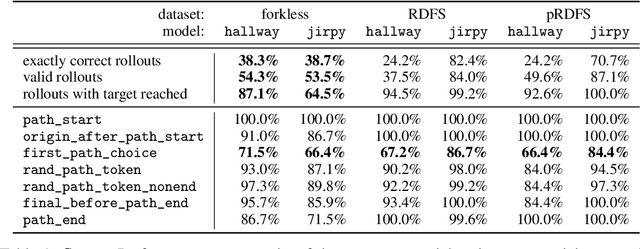
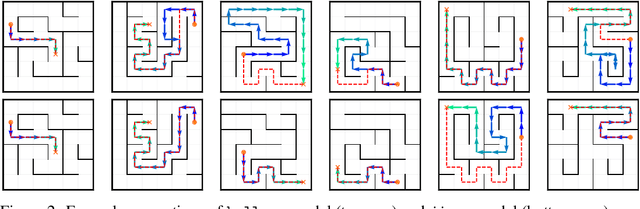
Transformer models underpin many recent advances in practical machine learning applications, yet understanding their internal behavior continues to elude researchers. Given the size and complexity of these models, forming a comprehensive picture of their inner workings remains a significant challenge. To this end, we set out to understand small transformer models in a more tractable setting: that of solving mazes. In this work, we focus on the abstractions formed by these models and find evidence for the consistent emergence of structured internal representations of maze topology and valid paths. We demonstrate this by showing that the residual stream of only a single token can be linearly decoded to faithfully reconstruct the entire maze. We also find that the learned embeddings of individual tokens have spatial structure. Furthermore, we take steps towards deciphering the circuity of path-following by identifying attention heads (dubbed $\textit{adjacency heads}$), which are implicated in finding valid subsequent tokens.

Training Dynamics of Contextual N-Grams in Language Models

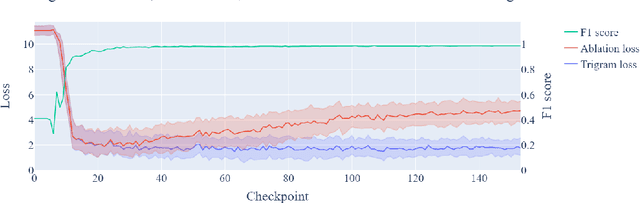
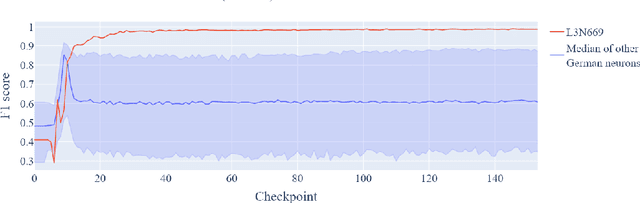
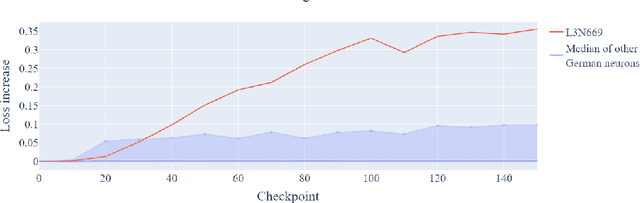
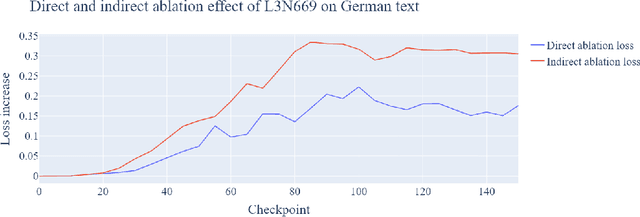
Prior work has shown the existence of contextual neurons in language models, including a neuron that activates on German text. We show that this neuron exists within a broader contextual n-gram circuit: we find late layer neurons which recognize and continue n-grams common in German text, but which only activate if the German neuron is active. We investigate the formation of this circuit throughout training and find that it is an example of what we call a second-order circuit. In particular, both the constituent n-gram circuits and the German detection circuit which culminates in the German neuron form with independent functions early in training - the German detection circuit partially through modeling German unigram statistics, and the n-grams by boosting appropriate completions. Only after both circuits have already formed do they fit together into a second-order circuit. Contrary to the hypotheses presented in prior work, we find that the contextual n-gram circuit forms gradually rather than in a sudden phase transition. We further present a range of anomalous observations such as a simultaneous phase transition in many tasks coinciding with the learning rate warm-up, and evidence that many context neurons form simultaneously early in training but are later unlearned.

A Configurable Library for Generating and Manipulating Maze Datasets

Understanding how machine learning models respond to distributional shifts is a key research challenge. Mazes serve as an excellent testbed due to varied generation algorithms offering a nuanced platform to simulate both subtle and pronounced distributional shifts. To enable systematic investigations of model behavior on out-of-distribution data, we present $\texttt{maze-dataset}$, a comprehensive library for generating, processing, and visualizing datasets consisting of maze-solving tasks. With this library, researchers can easily create datasets, having extensive control over the generation algorithm used, the parameters fed to the algorithm of choice, and the filters that generated mazes must satisfy. Furthermore, it supports multiple output formats, including rasterized and text-based, catering to convolutional neural networks and autoregressive transformer models. These formats, along with tools for visualizing and converting between them, ensure versatility and adaptability in research applications.