Xiaoli Fern
Neural Networks Learn Statistics of Increasing Complexity
Feb 13, 2024



Abstract:The distributional simplicity bias (DSB) posits that neural networks learn low-order moments of the data distribution first, before moving on to higher-order correlations. In this work, we present compelling new evidence for the DSB by showing that networks automatically learn to perform well on maximum-entropy distributions whose low-order statistics match those of the training set early in training, then lose this ability later. We also extend the DSB to discrete domains by proving an equivalence between token $n$-gram frequencies and the moments of embedding vectors, and by finding empirical evidence for the bias in LLMs. Finally we use optimal transport methods to surgically edit the low-order statistics of one class to match those of another, and show that early-training networks treat the edited samples as if they were drawn from the target class. Code is available at https://github.com/EleutherAI/features-across-time.
Non-equilibrium molecular geometries in graph neural networks
Mar 07, 2022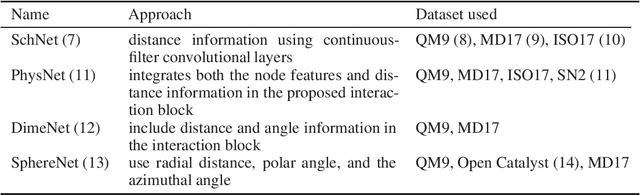
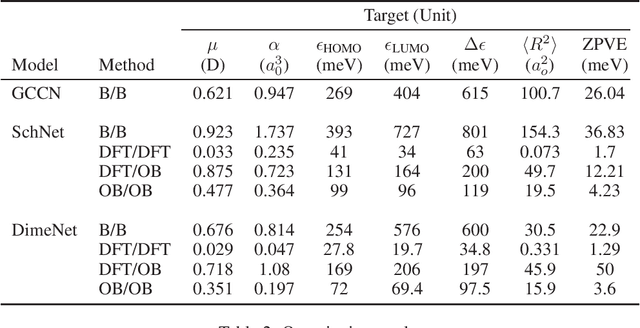
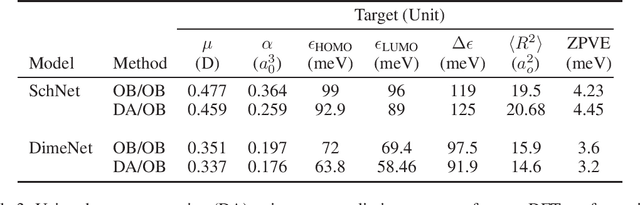
Abstract:Graph neural networks have become a powerful framework for learning complex structure-property relationships and fast screening of chemical compounds. Recently proposed methods have demonstrated that using 3D geometry information of the molecule along with the bonding structure can lead to more accurate prediction on a wide range of properties. A common practice is to use 3D geometries computed through density functional theory (DFT) for both training and testing of models. However, the computational time needed for DFT calculations can be prohibitively large. Moreover, many of the properties that we aim to predict can often be obtained with little or no overhead on top of the DFT calculations used to produce the 3D geometry information, voiding the need for a predictive model. To be practically useful for high-throughput chemical screening and drug discovery, it is desirable to work with 3D geometries obtained using less-accurate but much more efficient non-DFT methods. In this work we investigate the impact of using non-DFT conformations in the training and the testing of existing models and propose a data augmentation method for improving the prediction accuracy of classical forcefield-derived geometries.
Towards explainable message passing networks for predicting carbon dioxide adsorption in metal-organic frameworks
Dec 02, 2020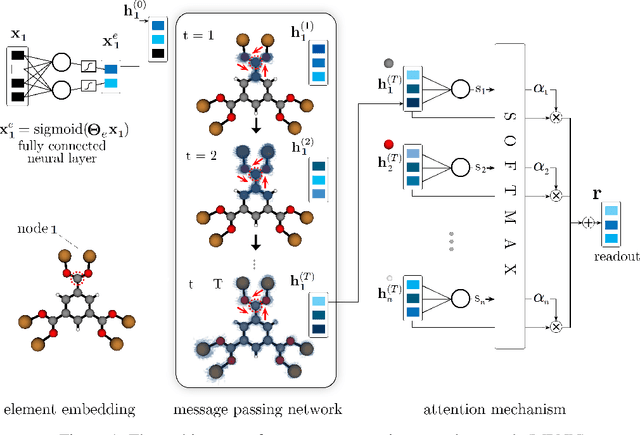
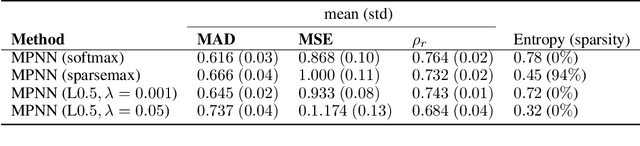
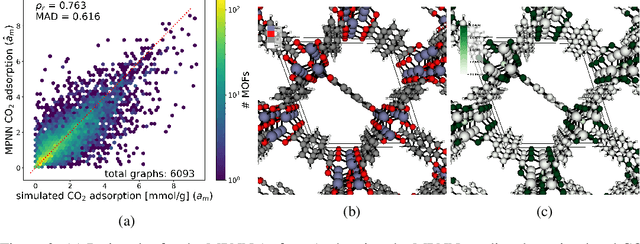
Abstract:Metal-organic framework (MOFs) are nanoporous materials that could be used to capture carbon dioxide from the exhaust gas of fossil fuel power plants to mitigate climate change. In this work, we design and train a message passing neural network (MPNN) to predict simulated CO$_2$ adsorption in MOFs. Towards providing insights into what substructures of the MOFs are important for the prediction, we introduce a soft attention mechanism into the readout function that quantifies the contributions of the node representations towards the graph representations. We investigate different mechanisms for sparse attention to ensure only the most relevant substructures are identified.
Learning Scripts as Hidden Markov Models
Sep 11, 2018


Abstract:Scripts have been proposed to model the stereotypical event sequences found in narratives. They can be applied to make a variety of inferences including filling gaps in the narratives and resolving ambiguous references. This paper proposes the first formal framework for scripts based on Hidden Markov Models (HMMs). Our framework supports robust inference and learning algorithms, which are lacking in previous clustering models. We develop an algorithm for structure and parameter learning based on Expectation Maximization and evaluate it on a number of natural datasets. The results show that our algorithm is superior to several informed baselines for predicting missing events in partial observation sequences.
Event Detection with Neural Networks: A Rigorous Empirical Evaluation
Aug 26, 2018



Abstract:Detecting events and classifying them into predefined types is an important step in knowledge extraction from natural language texts. While the neural network models have generally led the state-of-the-art, the differences in performance between different architectures have not been rigorously studied. In this paper we present a novel GRU-based model that combines syntactic information along with temporal structure through an attention mechanism. We show that it is competitive with other neural network architectures through empirical evaluations under different random initializations and training-validation-test splits of ACE2005 dataset.
A Lipschitz Exploration-Exploitation Scheme for Bayesian Optimization
Jul 16, 2013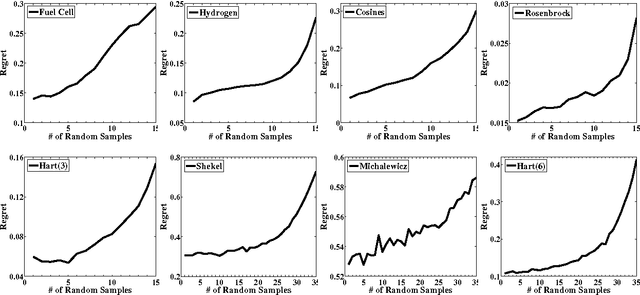

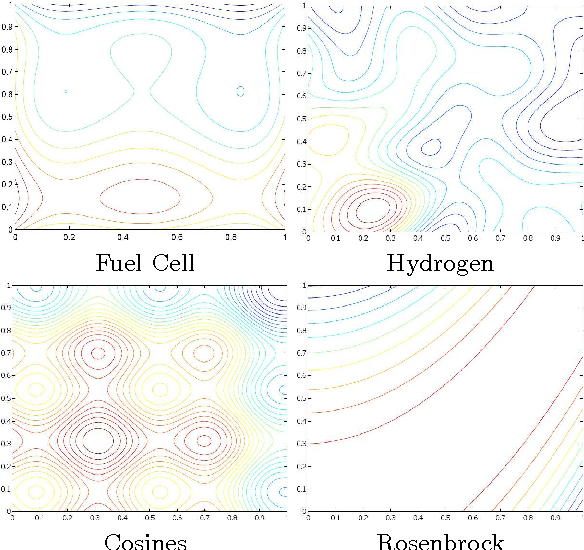
Abstract:The problem of optimizing unknown costly-to-evaluate functions has been studied for a long time in the context of Bayesian Optimization. Algorithms in this field aim to find the optimizer of the function by asking only a few function evaluations at locations carefully selected based on a posterior model. In this paper, we assume the unknown function is Lipschitz continuous. Leveraging the Lipschitz property, we propose an algorithm with a distinct exploration phase followed by an exploitation phase. The exploration phase aims to select samples that shrink the search space as much as possible. The exploitation phase then focuses on the reduced search space and selects samples closest to the optimizer. Considering the Expected Improvement (EI) as a baseline, we empirically show that the proposed algorithm significantly outperforms EI.
Hybrid Batch Bayesian Optimization
May 01, 2012

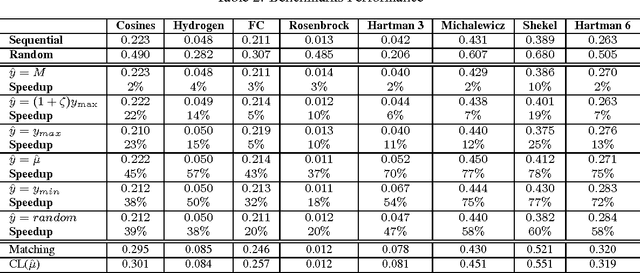
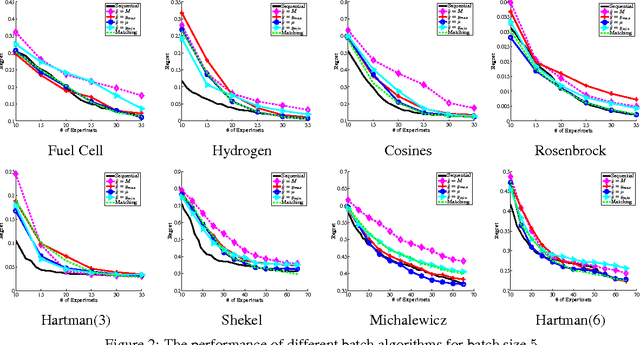
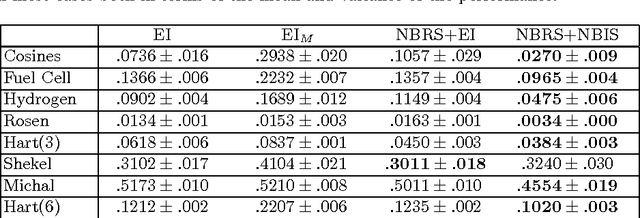
Abstract:Bayesian Optimization aims at optimizing an unknown non-convex/concave function that is costly to evaluate. We are interested in application scenarios where concurrent function evaluations are possible. Under such a setting, BO could choose to either sequentially evaluate the function, one input at a time and wait for the output of the function before making the next selection, or evaluate the function at a batch of multiple inputs at once. These two different settings are commonly referred to as the sequential and batch settings of Bayesian Optimization. In general, the sequential setting leads to better optimization performance as each function evaluation is selected with more information, whereas the batch setting has an advantage in terms of the total experimental time (the number of iterations). In this work, our goal is to combine the strength of both settings. Specifically, we systematically analyze Bayesian optimization using Gaussian process as the posterior estimator and provide a hybrid algorithm that, based on the current state, dynamically switches between a sequential policy and a batch policy with variable batch sizes. We provide theoretical justification for our algorithm and present experimental results on eight benchmark BO problems. The results show that our method achieves substantial speedup (up to %78) compared to a pure sequential policy, without suffering any significant performance loss.
Dynamic Batch Bayesian Optimization
Oct 14, 2011
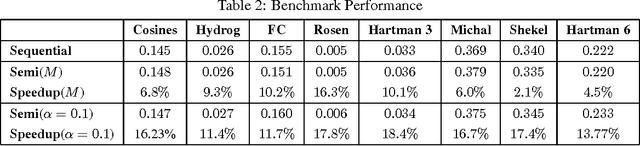
Abstract:Bayesian optimization (BO) algorithms try to optimize an unknown function that is expensive to evaluate using minimum number of evaluations/experiments. Most of the proposed algorithms in BO are sequential, where only one experiment is selected at each iteration. This method can be time inefficient when each experiment takes a long time and more than one experiment can be ran concurrently. On the other hand, requesting a fix-sized batch of experiments at each iteration causes performance inefficiency in BO compared to the sequential policies. In this paper, we present an algorithm that asks a batch of experiments at each time step t where the batch size p_t is dynamically determined in each step. Our algorithm is based on the observation that the sequence of experiments selected by the sequential policy can sometimes be almost independent from each other. Our algorithm identifies such scenarios and request those experiments at the same time without degrading the performance. We evaluate our proposed method using the Expected Improvement policy and the results show substantial speedup with little impact on the performance in eight real and synthetic benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge