Javad Azimi
Oregon State University
A Lipschitz Exploration-Exploitation Scheme for Bayesian Optimization
Jul 16, 2013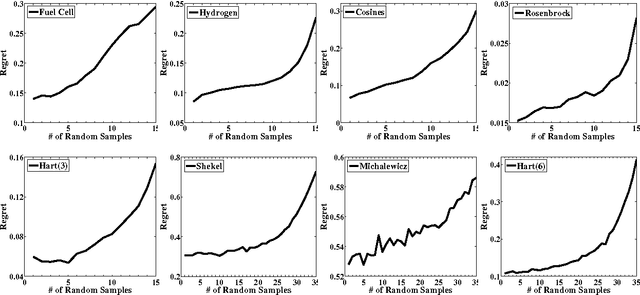

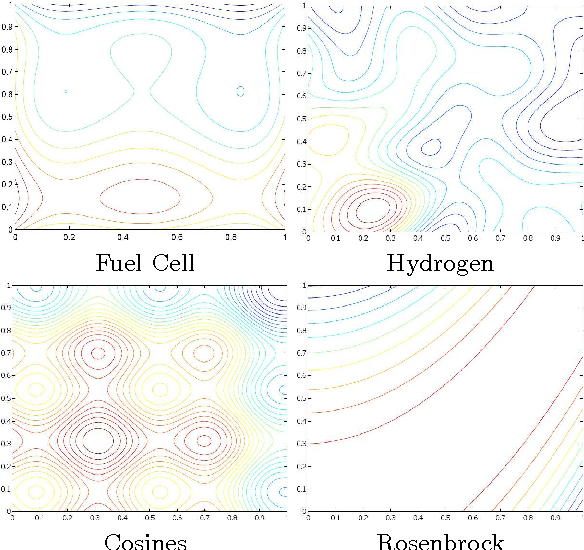
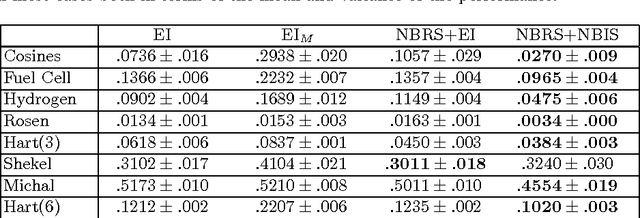
Abstract:The problem of optimizing unknown costly-to-evaluate functions has been studied for a long time in the context of Bayesian Optimization. Algorithms in this field aim to find the optimizer of the function by asking only a few function evaluations at locations carefully selected based on a posterior model. In this paper, we assume the unknown function is Lipschitz continuous. Leveraging the Lipschitz property, we propose an algorithm with a distinct exploration phase followed by an exploitation phase. The exploration phase aims to select samples that shrink the search space as much as possible. The exploitation phase then focuses on the reduced search space and selects samples closest to the optimizer. Considering the Expected Improvement (EI) as a baseline, we empirically show that the proposed algorithm significantly outperforms EI.
Batch Active Learning via Coordinated Matching
Jun 27, 2012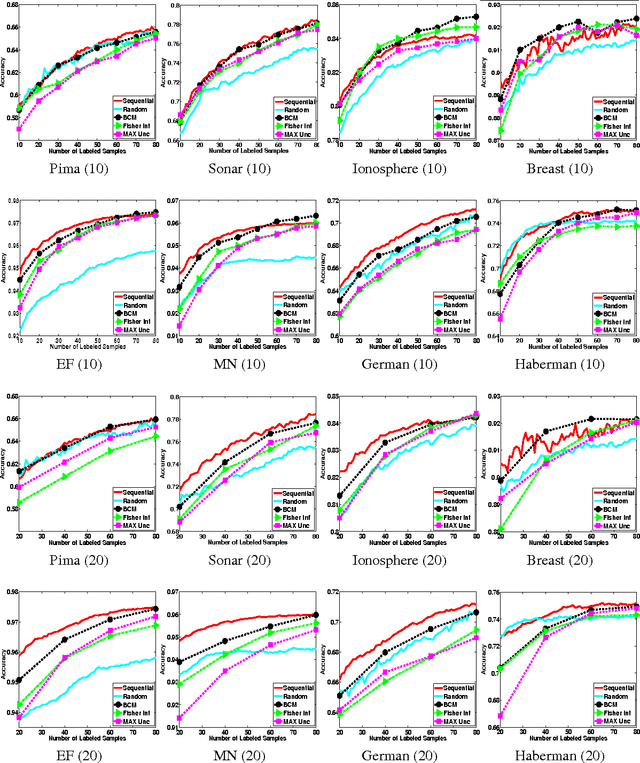
Abstract:Most prior work on active learning of classifiers has focused on sequentially selecting one unlabeled example at a time to be labeled in order to reduce the overall labeling effort. In many scenarios, however, it is desirable to label an entire batch of examples at once, for example, when labels can be acquired in parallel. This motivates us to study batch active learning, which iteratively selects batches of $k>1$ examples to be labeled. We propose a novel batch active learning method that leverages the availability of high-quality and efficient sequential active-learning policies by attempting to approximate their behavior when applied for $k$ steps. Specifically, our algorithm first uses Monte-Carlo simulation to estimate the distribution of unlabeled examples selected by a sequential policy over $k$ step executions. The algorithm then attempts to select a set of $k$ examples that best matches this distribution, leading to a combinatorial optimization problem that we term "bounded coordinated matching". While we show this problem is NP-hard in general, we give an efficient greedy solution, which inherits approximation bounds from supermodular minimization theory. Our experimental results on eight benchmark datasets show that the proposed approach is highly effective
Hybrid Batch Bayesian Optimization
May 01, 2012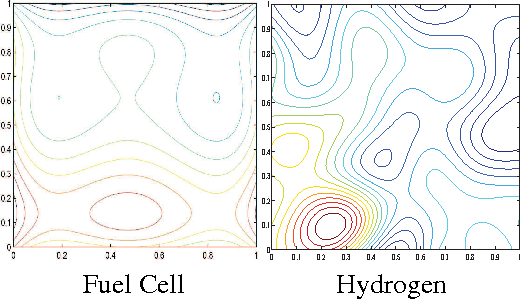

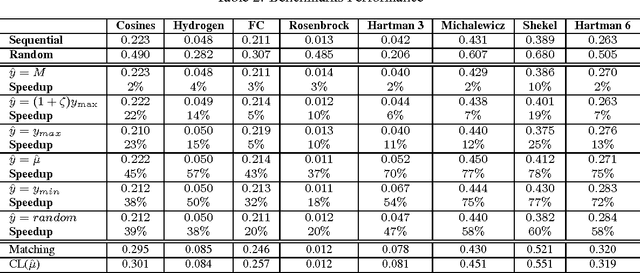
Abstract:Bayesian Optimization aims at optimizing an unknown non-convex/concave function that is costly to evaluate. We are interested in application scenarios where concurrent function evaluations are possible. Under such a setting, BO could choose to either sequentially evaluate the function, one input at a time and wait for the output of the function before making the next selection, or evaluate the function at a batch of multiple inputs at once. These two different settings are commonly referred to as the sequential and batch settings of Bayesian Optimization. In general, the sequential setting leads to better optimization performance as each function evaluation is selected with more information, whereas the batch setting has an advantage in terms of the total experimental time (the number of iterations). In this work, our goal is to combine the strength of both settings. Specifically, we systematically analyze Bayesian optimization using Gaussian process as the posterior estimator and provide a hybrid algorithm that, based on the current state, dynamically switches between a sequential policy and a batch policy with variable batch sizes. We provide theoretical justification for our algorithm and present experimental results on eight benchmark BO problems. The results show that our method achieves substantial speedup (up to %78) compared to a pure sequential policy, without suffering any significant performance loss.
Dynamic Batch Bayesian Optimization
Oct 14, 2011
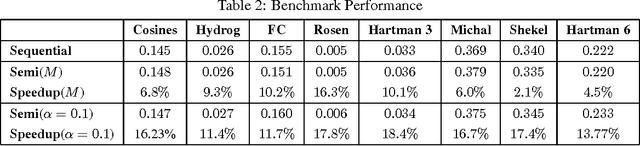
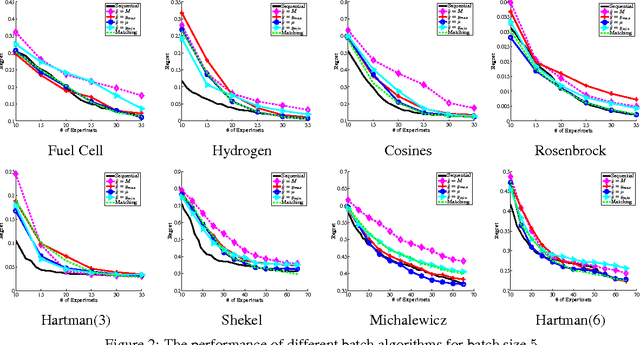
Abstract:Bayesian optimization (BO) algorithms try to optimize an unknown function that is expensive to evaluate using minimum number of evaluations/experiments. Most of the proposed algorithms in BO are sequential, where only one experiment is selected at each iteration. This method can be time inefficient when each experiment takes a long time and more than one experiment can be ran concurrently. On the other hand, requesting a fix-sized batch of experiments at each iteration causes performance inefficiency in BO compared to the sequential policies. In this paper, we present an algorithm that asks a batch of experiments at each time step t where the batch size p_t is dynamically determined in each step. Our algorithm is based on the observation that the sequence of experiments selected by the sequential policy can sometimes be almost independent from each other. Our algorithm identifies such scenarios and request those experiments at the same time without degrading the performance. We evaluate our proposed method using the Expected Improvement policy and the results show substantial speedup with little impact on the performance in eight real and synthetic benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge