A Principled Approach to Learning Stochastic Representations for Privacy in Deep Neural Inference

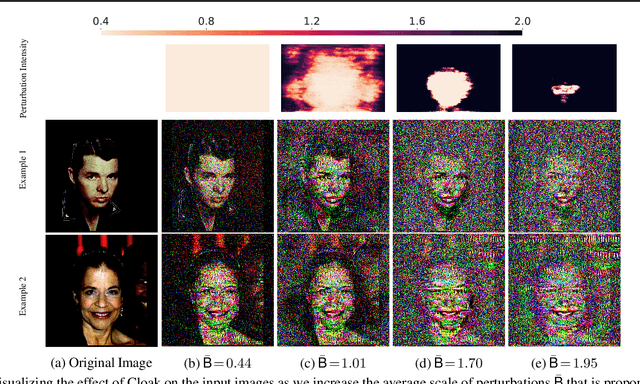
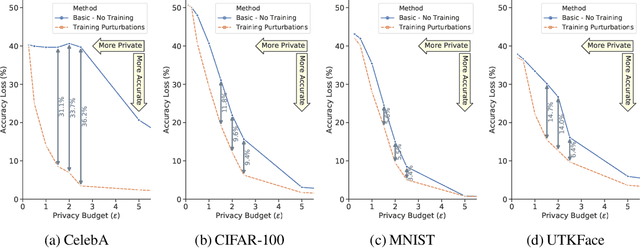
INFerence-as-a-Service (INFaaS) in the cloud has enabled the prevalent use of Deep Neural Networks (DNNs) in home automation, targeted advertising, machine vision, etc. The cloud receives the inference request as a raw input, containing a rich set of private information, that can be misused or leaked, possibly inadvertently. This prevalent setting can compromise the privacy of users during the inference phase. This paper sets out to provide a principled approach, dubbed Cloak, that finds optimal stochastic perturbations to obfuscate the private data before it is sent to the cloud. To this end, Cloak reduces the information content of the transmitted data while conserving the essential pieces that enable the request to be serviced accurately. The key idea is formulating the discovery of this stochasticity as an offline gradient-based optimization problem that reformulates a pre-trained DNN (with optimized known weights) as an analytical function of the stochastic perturbations. Using Laplace distribution as a parametric model for the stochastic perturbations, Cloak learns the optimal parameters using gradient descent and Monte Carlo sampling. This set of optimized Laplace distributions further guarantee that the injected stochasticity satisfies the -differential privacy criterion. Experimental evaluations with real-world datasets show that, on average, the injected stochasticity can reduce the information content in the input data by 80.07%, while incurring 7.12% accuracy loss.

Clustering Partially Observed Graphs via Convex Optimization

This paper considers the problem of clustering a partially observed unweighted graph---i.e., one where for some node pairs we know there is an edge between them, for some others we know there is no edge, and for the remaining we do not know whether or not there is an edge. We want to organize the nodes into disjoint clusters so that there is relatively dense (observed) connectivity within clusters, and sparse across clusters. We take a novel yet natural approach to this problem, by focusing on finding the clustering that minimizes the number of "disagreements"---i.e., the sum of the number of (observed) missing edges within clusters, and (observed) present edges across clusters. Our algorithm uses convex optimization; its basis is a reduction of disagreement minimization to the problem of recovering an (unknown) low-rank matrix and an (unknown) sparse matrix from their partially observed sum. We evaluate the performance of our algorithm on the classical Planted Partition/Stochastic Block Model. Our main theorem provides sufficient conditions for the success of our algorithm as a function of the minimum cluster size, edge density and observation probability; in particular, the results characterize the tradeoff between the observation probability and the edge density gap. When there are a constant number of clusters of equal size, our results are optimal up to logarithmic factors.

A Lipschitz Exploration-Exploitation Scheme for Bayesian Optimization

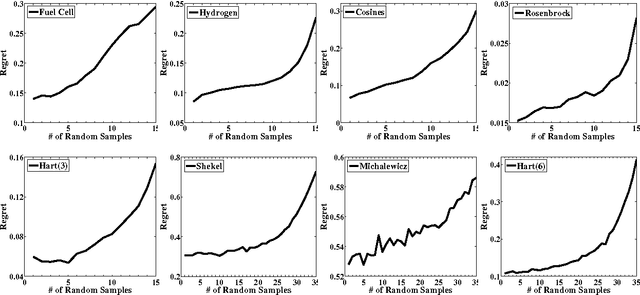
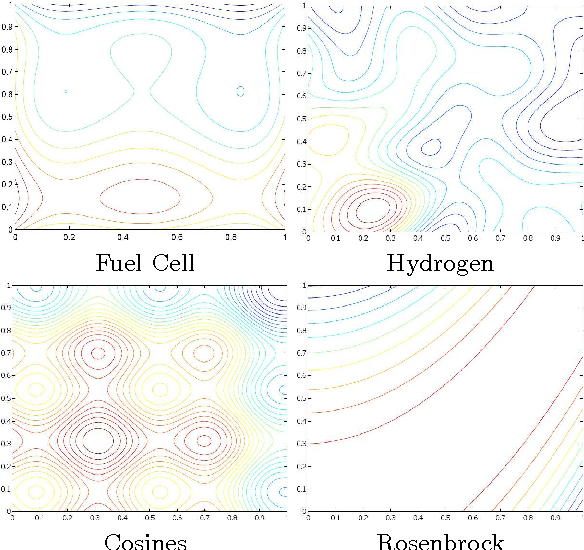
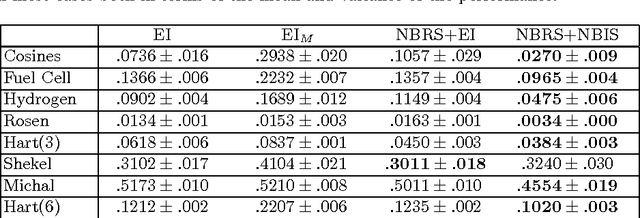
The problem of optimizing unknown costly-to-evaluate functions has been studied for a long time in the context of Bayesian Optimization. Algorithms in this field aim to find the optimizer of the function by asking only a few function evaluations at locations carefully selected based on a posterior model. In this paper, we assume the unknown function is Lipschitz continuous. Leveraging the Lipschitz property, we propose an algorithm with a distinct exploration phase followed by an exploitation phase. The exploration phase aims to select samples that shrink the search space as much as possible. The exploitation phase then focuses on the reduced search space and selects samples closest to the optimizer. Considering the Expected Improvement (EI) as a baseline, we empirically show that the proposed algorithm significantly outperforms EI.

Scalable Audience Reach Estimation in Real-time Online Advertising

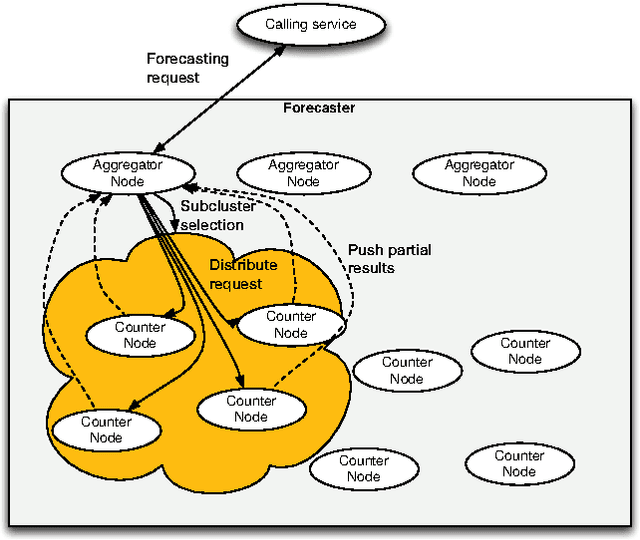
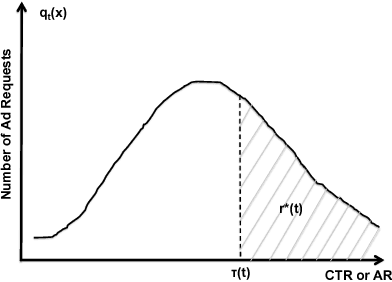
Online advertising has been introduced as one of the most efficient methods of advertising throughout the recent years. Yet, advertisers are concerned about the efficiency of their online advertising campaigns and consequently, would like to restrict their ad impressions to certain websites and/or certain groups of audience. These restrictions, known as targeting criteria, limit the reachability for better performance. This trade-off between reachability and performance illustrates a need for a forecasting system that can quickly predict/estimate (with good accuracy) this trade-off. Designing such a system is challenging due to (a) the huge amount of data to process, and, (b) the need for fast and accurate estimates. In this paper, we propose a distributed fault tolerant system that can generate such estimates fast with good accuracy. The main idea is to keep a small representative sample in memory across multiple machines and formulate the forecasting problem as queries against the sample. The key challenge is to find the best strata across the past data, perform multivariate stratified sampling while ensuring fuzzy fall-back to cover the small minorities. Our results show a significant improvement over the uniform and simple stratified sampling strategies which are currently widely used in the industry.

Real Time Bid Optimization with Smooth Budget Delivery in Online Advertising

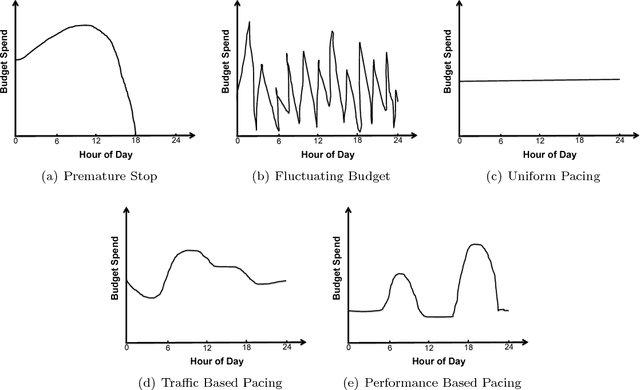
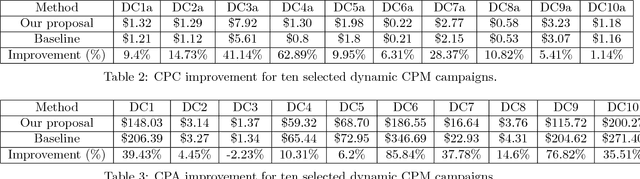
Today, billions of display ad impressions are purchased on a daily basis through a public auction hosted by real time bidding (RTB) exchanges. A decision has to be made for advertisers to submit a bid for each selected RTB ad request in milliseconds. Restricted by the budget, the goal is to buy a set of ad impressions to reach as many targeted users as possible. A desired action (conversion), advertiser specific, includes purchasing a product, filling out a form, signing up for emails, etc. In addition, advertisers typically prefer to spend their budget smoothly over the time in order to reach a wider range of audience accessible throughout a day and have a sustainable impact. However, since the conversions occur rarely and the occurrence feedback is normally delayed, it is very challenging to achieve both budget and performance goals at the same time. In this paper, we present an online approach to the smooth budget delivery while optimizing for the conversion performance. Our algorithm tries to select high quality impressions and adjust the bid price based on the prior performance distribution in an adaptive manner by distributing the budget optimally across time. Our experimental results from real advertising campaigns demonstrate the effectiveness of our proposed approach.

A New Greedy Algorithm for Multiple Sparse Regression

This paper proposes a new algorithm for multiple sparse regression in high dimensions, where the task is to estimate the support and values of several (typically related) sparse vectors from a few noisy linear measurements. Our algorithm is a "forward-backward" greedy procedure that -- uniquely -- operates on two distinct classes of objects. In particular, we organize our target sparse vectors as a matrix; our algorithm involves iterative addition and removal of both (a) individual elements, and (b) entire rows (corresponding to shared features), of the matrix. Analytically, we establish that our algorithm manages to recover the supports (exactly) and values (approximately) of the sparse vectors, under assumptions similar to existing approaches based on convex optimization. However, our algorithm has a much smaller computational complexity. Perhaps most interestingly, it is seen empirically to require visibly fewer samples. Ours represents the first attempt to extend greedy algorithms to the class of models that can only/best be represented by a combination of component structural assumptions (sparse and group-sparse, in our case).

Learning the Dependence Graph of Time Series with Latent Factors

This paper considers the problem of learning, from samples, the dependency structure of a system of linear stochastic differential equations, when some of the variables are latent. In particular, we observe the time evolution of some variables, and never observe other variables; from this, we would like to find the dependency structure between the observed variables - separating out the spurious interactions caused by the (marginalizing out of the) latent variables' time series. We develop a new method, based on convex optimization, to do so in the case when the number of latent variables is smaller than the number of observed ones. For the case when the dependency structure between the observed variables is sparse, we theoretically establish a high-dimensional scaling result for structure recovery. We verify our theoretical result with both synthetic and real data (from the stock market).

Hybrid Batch Bayesian Optimization

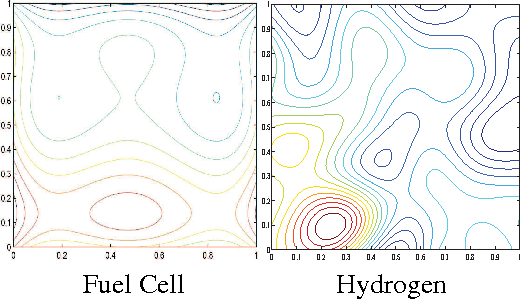
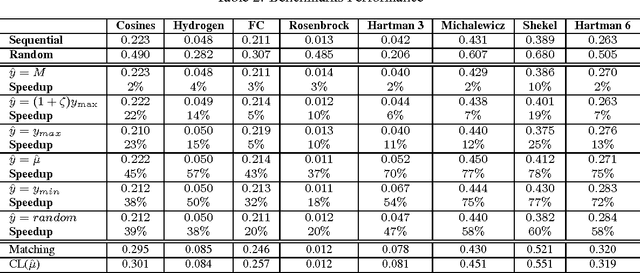
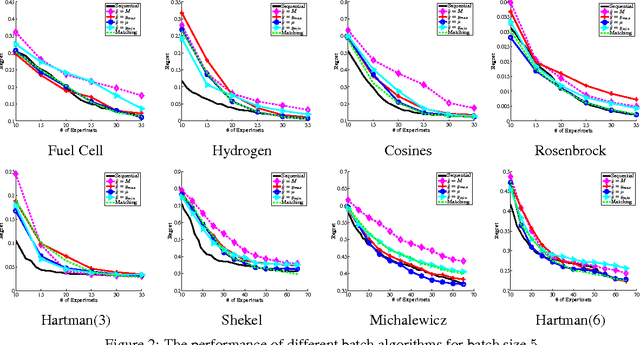
Bayesian Optimization aims at optimizing an unknown non-convex/concave function that is costly to evaluate. We are interested in application scenarios where concurrent function evaluations are possible. Under such a setting, BO could choose to either sequentially evaluate the function, one input at a time and wait for the output of the function before making the next selection, or evaluate the function at a batch of multiple inputs at once. These two different settings are commonly referred to as the sequential and batch settings of Bayesian Optimization. In general, the sequential setting leads to better optimization performance as each function evaluation is selected with more information, whereas the batch setting has an advantage in terms of the total experimental time (the number of iterations). In this work, our goal is to combine the strength of both settings. Specifically, we systematically analyze Bayesian optimization using Gaussian process as the posterior estimator and provide a hybrid algorithm that, based on the current state, dynamically switches between a sequential policy and a batch policy with variable batch sizes. We provide theoretical justification for our algorithm and present experimental results on eight benchmark BO problems. The results show that our method achieves substantial speedup (up to %78) compared to a pure sequential policy, without suffering any significant performance loss.

Clustering using Max-norm Constrained Optimization

We suggest using the max-norm as a convex surrogate constraint for clustering. We show how this yields a better exact cluster recovery guarantee than previously suggested nuclear-norm relaxation, and study the effectiveness of our method, and other related convex relaxations, compared to other clustering approaches.

High-dimensional Sparse Inverse Covariance Estimation using Greedy Methods

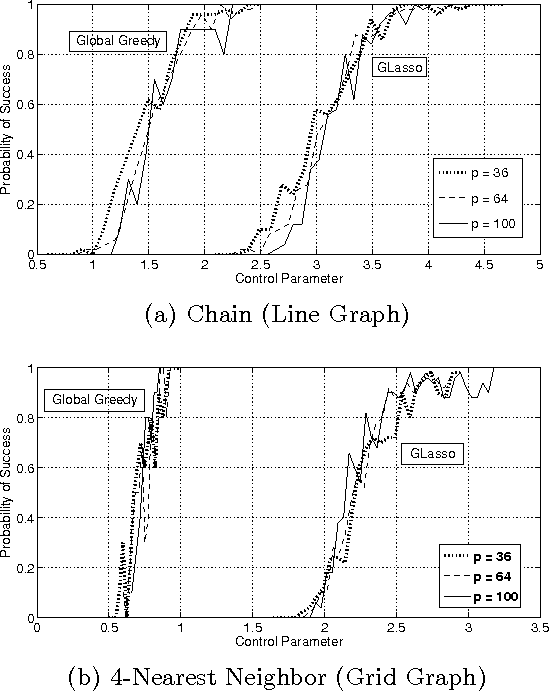
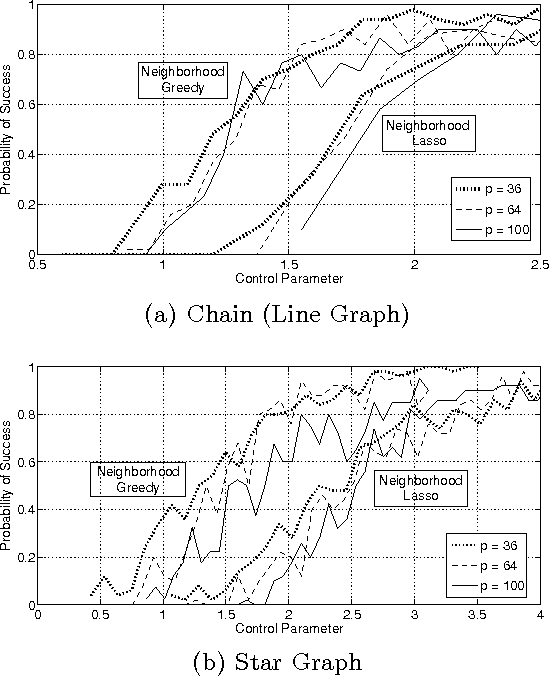
In this paper we consider the task of estimating the non-zero pattern of the sparse inverse covariance matrix of a zero-mean Gaussian random vector from a set of iid samples. Note that this is also equivalent to recovering the underlying graph structure of a sparse Gaussian Markov Random Field (GMRF). We present two novel greedy approaches to solving this problem. The first estimates the non-zero covariates of the overall inverse covariance matrix using a series of global forward and backward greedy steps. The second estimates the neighborhood of each node in the graph separately, again using greedy forward and backward steps, and combines the intermediate neighborhoods to form an overall estimate. The principal contribution of this paper is a rigorous analysis of the sparsistency, or consistency in recovering the sparsity pattern of the inverse covariance matrix. Surprisingly, we show that both the local and global greedy methods learn the full structure of the model with high probability given just $O(d\log(p))$ samples, which is a \emph{significant} improvement over state of the art $\ell_1$-regularized Gaussian MLE (Graphical Lasso) that requires $O(d^2\log(p))$ samples. Moreover, the restricted eigenvalue and smoothness conditions imposed by our greedy methods are much weaker than the strong irrepresentable conditions required by the $\ell_1$-regularization based methods. We corroborate our results with extensive simulations and examples, comparing our local and global greedy methods to the $\ell_1$-regularized Gaussian MLE as well as the Neighborhood Greedy method to that of nodewise $\ell_1$-regularized linear regression (Neighborhood Lasso).