High-dimensional Sparse Inverse Covariance Estimation using Greedy Methods
Paper and Code
Dec 29, 2011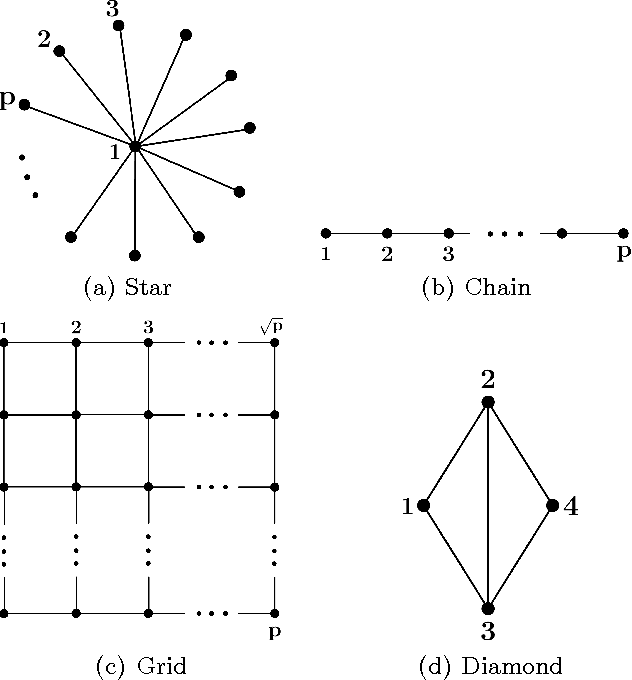
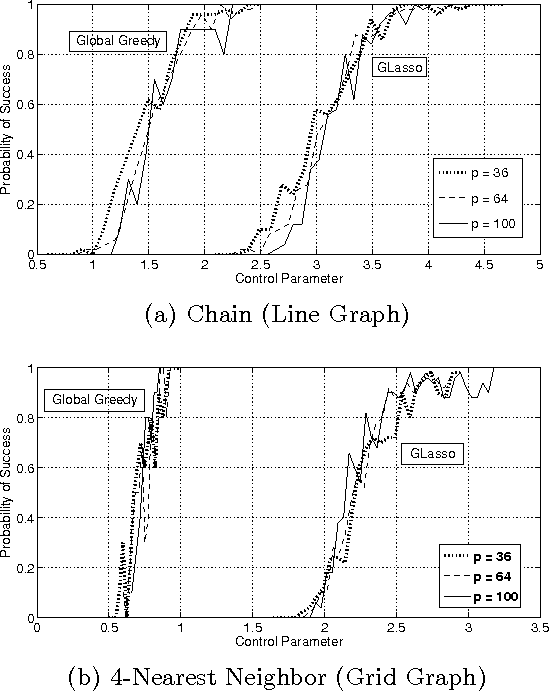
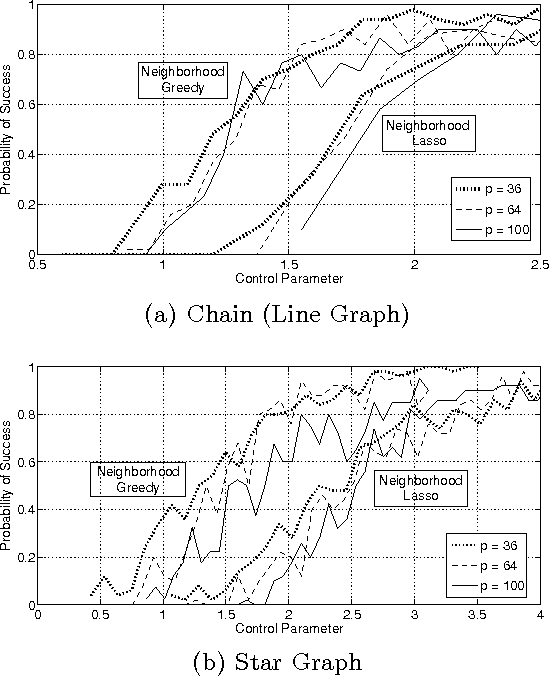
In this paper we consider the task of estimating the non-zero pattern of the sparse inverse covariance matrix of a zero-mean Gaussian random vector from a set of iid samples. Note that this is also equivalent to recovering the underlying graph structure of a sparse Gaussian Markov Random Field (GMRF). We present two novel greedy approaches to solving this problem. The first estimates the non-zero covariates of the overall inverse covariance matrix using a series of global forward and backward greedy steps. The second estimates the neighborhood of each node in the graph separately, again using greedy forward and backward steps, and combines the intermediate neighborhoods to form an overall estimate. The principal contribution of this paper is a rigorous analysis of the sparsistency, or consistency in recovering the sparsity pattern of the inverse covariance matrix. Surprisingly, we show that both the local and global greedy methods learn the full structure of the model with high probability given just $O(d\log(p))$ samples, which is a \emph{significant} improvement over state of the art $\ell_1$-regularized Gaussian MLE (Graphical Lasso) that requires $O(d^2\log(p))$ samples. Moreover, the restricted eigenvalue and smoothness conditions imposed by our greedy methods are much weaker than the strong irrepresentable conditions required by the $\ell_1$-regularization based methods. We corroborate our results with extensive simulations and examples, comparing our local and global greedy methods to the $\ell_1$-regularized Gaussian MLE as well as the Neighborhood Greedy method to that of nodewise $\ell_1$-regularized linear regression (Neighborhood Lasso).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge