Large-scale Collaborative Filtering with Product Embeddings

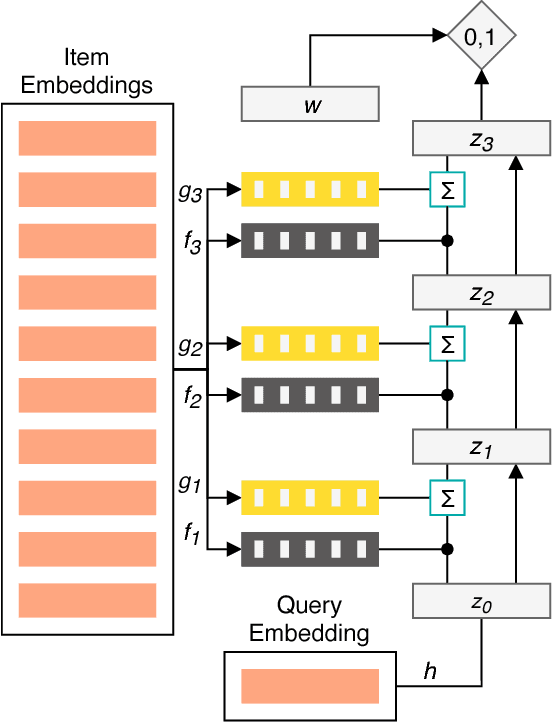
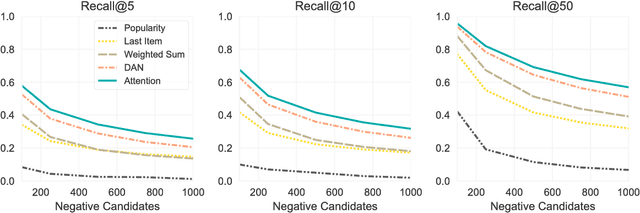
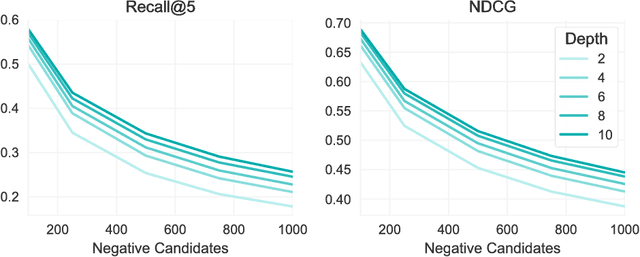
The application of machine learning techniques to large-scale personalized recommendation problems is a challenging task. Such systems must make sense of enormous amounts of implicit feedback in order to understand user preferences across numerous product categories. This paper presents a deep learning based solution to this problem within the collaborative filtering with implicit feedback framework. Our approach combines neural attention mechanisms, which allow for context dependent weighting of past behavioral signals, with representation learning techniques to produce models which obtain extremely high coverage, can easily incorporate new information as it becomes available, and are computationally efficient. Offline experiments demonstrate significant performance improvements when compared to several alternative methods from the literature. Results from an online setting show that the approach compares favorably with current production techniques used to produce personalized product recommendations.

High-dimensional Sparse Inverse Covariance Estimation using Greedy Methods

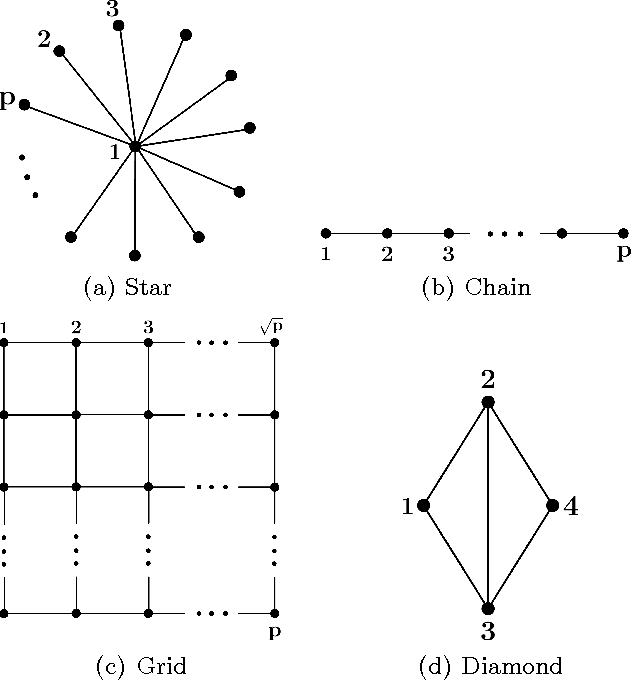
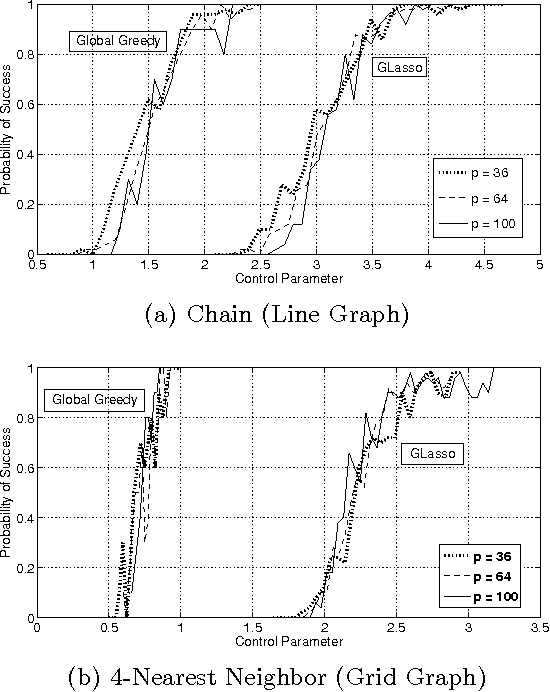
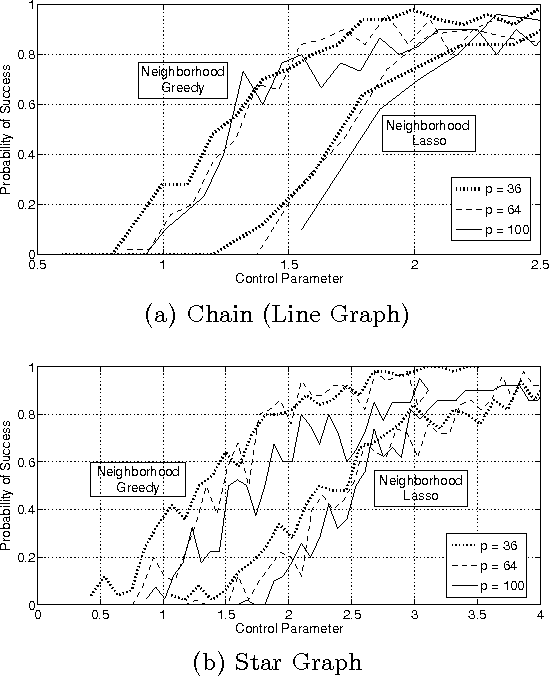
In this paper we consider the task of estimating the non-zero pattern of the sparse inverse covariance matrix of a zero-mean Gaussian random vector from a set of iid samples. Note that this is also equivalent to recovering the underlying graph structure of a sparse Gaussian Markov Random Field (GMRF). We present two novel greedy approaches to solving this problem. The first estimates the non-zero covariates of the overall inverse covariance matrix using a series of global forward and backward greedy steps. The second estimates the neighborhood of each node in the graph separately, again using greedy forward and backward steps, and combines the intermediate neighborhoods to form an overall estimate. The principal contribution of this paper is a rigorous analysis of the sparsistency, or consistency in recovering the sparsity pattern of the inverse covariance matrix. Surprisingly, we show that both the local and global greedy methods learn the full structure of the model with high probability given just $O(d\log(p))$ samples, which is a \emph{significant} improvement over state of the art $\ell_1$-regularized Gaussian MLE (Graphical Lasso) that requires $O(d^2\log(p))$ samples. Moreover, the restricted eigenvalue and smoothness conditions imposed by our greedy methods are much weaker than the strong irrepresentable conditions required by the $\ell_1$-regularization based methods. We corroborate our results with extensive simulations and examples, comparing our local and global greedy methods to the $\ell_1$-regularized Gaussian MLE as well as the Neighborhood Greedy method to that of nodewise $\ell_1$-regularized linear regression (Neighborhood Lasso).