Denoising neural networks for magnetic resonance spectroscopy

In many scientific applications, measured time series are corrupted by noise or distortions. Traditional denoising techniques often fail to recover the signal of interest, particularly when the signal-to-noise ratio is low or when certain assumptions on the signal and noise are violated. In this work, we demonstrate that deep learning-based denoising methods can outperform traditional techniques while exhibiting greater robustness to variation in noise and signal characteristics. Our motivating example is magnetic resonance spectroscopy, in which a primary goal is to detect the presence of short-duration, low-amplitude radio frequency signals that are often obscured by strong interference that can be difficult to separate from the signal using traditional methods. We explore various deep learning architecture choices to capture the inherently complex-valued nature of magnetic resonance signals. On both synthetic and experimental data, we show that our deep learning-based approaches can exceed performance of traditional techniques, providing a powerful new class of methods for analysis of scientific time series data.

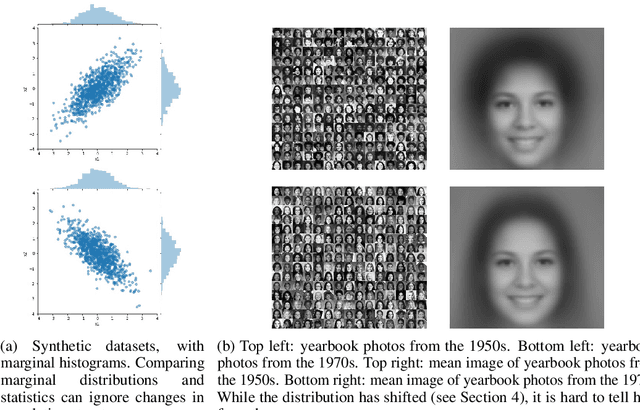
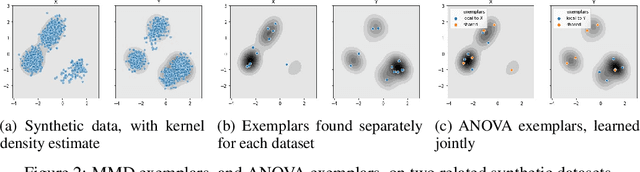
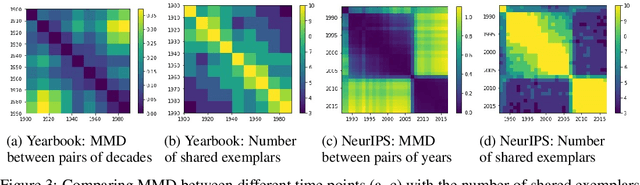
ANOVA exemplars for understanding data drift

The distributions underlying complex datasets, such as images, text or tabular data, are often difficult to visualize in terms of summary statistics such as the mean or the marginal standard deviations. Instead, a small set of exemplars or prototypes---real or synthetic data points that are in some sense representative of the entire distribution---can be used to provide a human-interpretable summary of the distribution. In many situations, we are interested in understanding the \textit{difference} between two distributions. For example, we may be interested in identifying and characterizing data drift over time, or the difference between two related datasets. While exemplars are often more easily understood than high-dimensional summary statistics, they are harder to compare. To solve this problem, we introduce ANOVA exemplars. Rather than independently find exemplars $S_X$ and $S_Y$ for two datasets $X$ and $Y$, we aim to find exemplars that are both representative of $X$ and $Y$, and that maximize the overlap $|S_X\cap S_Y|$ between the two sets of exemplars. We can then use the differences between the two sets of exemplars to describe the difference between the distributions of $X$ and $Y$, in a concise, interpretable manner.

Distributed, partially collapsed MCMC for Bayesian Nonparametrics

Bayesian nonparametric (BNP) models provide elegant methods for discovering underlying latent features within a data set, but inference in such models can be slow. We exploit the fact that completely random measures, which commonly used models like the Dirichlet process and the beta-Bernoulli process can be expressed as, are decomposable into independent sub-measures. We use this decomposition to partition the latent measure into a finite measure containing only instantiated components, and an infinite measure containing all other components. We then select different inference algorithms for the two components: uncollapsed samplers mix well on the finite measure, while collapsed samplers mix well on the infinite, sparsely occupied tail. The resulting hybrid algorithm can be applied to a wide class of models, and can be easily distributed to allow scalable inference without sacrificing asymptotic convergence guarantees.

A Nonparametric Bayesian Model for Sparse Temporal Multigraphs

As the availability and importance of temporal interaction data--such as email communication--increases, it becomes increasingly important to understand the underlying structure that underpins these interactions. Often these interactions form a multigraph, where we might have multiple interactions between two entities. Such multigraphs tend to be sparse yet structured, and their distribution often evolves over time. Existing statistical models with interpretable parameters can capture some, but not all, of these properties. We propose a dynamic nonparametric model for interaction multigraphs that combines the sparsity of edge-exchangeable multigraphs with dynamic clustering patterns that tend to reinforce recent behavioral patterns. We show that our method yields improved held-out likelihood over stationary variants, and impressive predictive performance against a range of state-of-the-art dynamic graph models.

Avoiding Resentment Via Monotonic Fairness

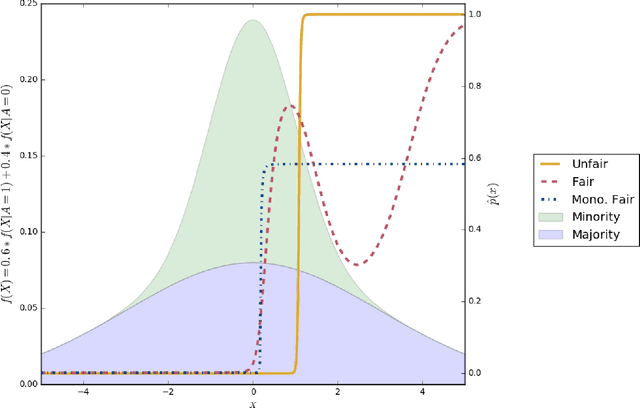
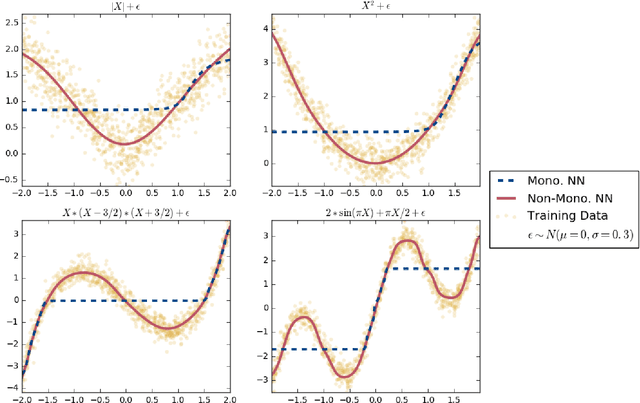
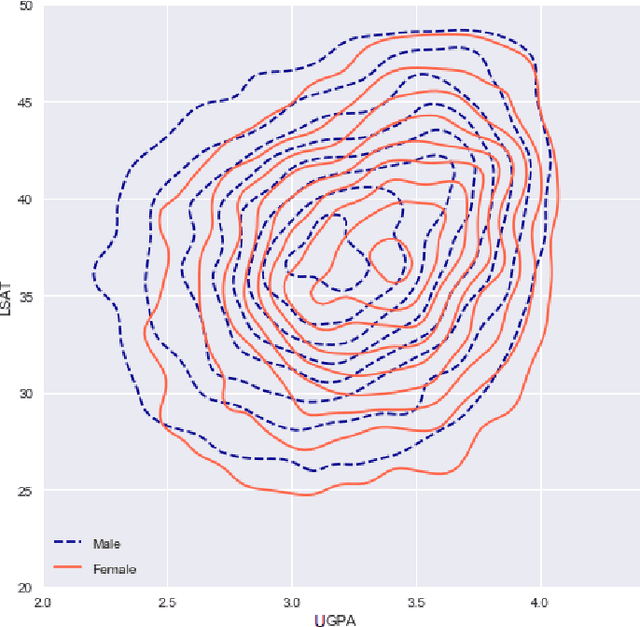
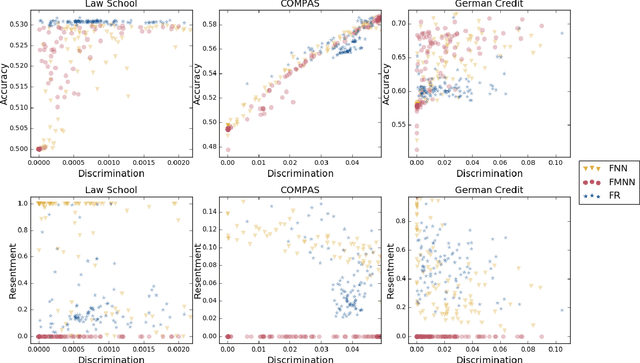
Classifiers that achieve demographic balance by explicitly using protected attributes such as race or gender are often politically or culturally controversial due to their lack of individual fairness, i.e. individuals with similar qualifications will receive different outcomes. Individually and group fair decision criteria can produce counter-intuitive results, e.g. that the optimal constrained boundary may reject intuitively better candidates due to demographic imbalance in similar candidates. Both approaches can be seen as introducing individual resentment, where some individuals would have received a better outcome if they either belonged to a different demographic class and had the same qualifications, or if they remained in the same class but had objectively worse qualifications (e.g. lower test scores). We show that both forms of resentment can be avoided by using monotonically constrained machine learning models to create individually fair, demographically balanced classifiers.

Sequential Gaussian Processes for Online Learning of Nonstationary Functions

Many machine learning problems can be framed in the context of estimating functions, and often these are time-dependent functions that are estimated in real-time as observations arrive. Gaussian processes (GPs) are an attractive choice for modeling real-valued nonlinear functions due to their flexibility and uncertainty quantification. However, the typical GP regression model suffers from several drawbacks: i) Conventional GP inference scales $O(N^{3})$ with respect to the number of observations; ii) updating a GP model sequentially is not trivial; and iii) covariance kernels often enforce stationarity constraints on the function, while GPs with non-stationary covariance kernels are often intractable to use in practice. To overcome these issues, we propose an online sequential Monte Carlo algorithm to fit mixtures of GPs that capture non-stationary behavior while allowing for fast, distributed inference. By formulating hyperparameter optimization as a multi-armed bandit problem, we accelerate mixing for real time inference. Our approach empirically improves performance over state-of-the-art methods for online GP estimation in the context of prediction for simulated non-stationary data and hospital time series data.

A New Class of Time Dependent Latent Factor Models with Applications

In many applications, observed data are influenced by some combination of latent causes. For example, suppose sensors are placed inside a building to record responses such as temperature, humidity, power consumption and noise levels. These random, observed responses are typically affected by many unobserved, latent factors (or features) within the building such as the number of individuals, the turning on and off of electrical devices, power surges, etc. These latent factors are usually present for a contiguous period of time before disappearing; further, multiple factors could be present at a time. This paper develops new probabilistic methodology and inference methods for random object generation influenced by latent features exhibiting temporal persistence. Every datum is associated with subsets of a potentially infinite number of hidden, persistent features that account for temporal dynamics in an observation. The ensuing class of dynamic models constructed by adapting the Indian Buffet Process --- a probability measure on the space of random, unbounded binary matrices --- finds use in a variety of applications arising in operations, signal processing, biomedicine, marketing, image analysis, etc. Illustrations using synthetic and real data are provided.

Stochastic Blockmodels with Edge Information

Stochastic blockmodels allow us to represent networks in terms of a latent community structure, often yielding intuitions about the underlying social structure. Typically, this structure is inferred based only on a binary network representing the presence or absence of interactions between nodes, which limits the amount of information that can be extracted from the data. In practice, many interaction networks contain much more information about the relationship between two nodes. For example, in an email network, the volume of communication between two users and the content of that communication can give us information about both the strength and the nature of their relationship. In this paper, we propose the Topic Blockmodel, a stochastic blockmodel that uses a count-based topic model to capture the interaction modalities within and between latent communities. By explicitly incorporating information sent between nodes in our network representation, we are able to address questions of interest in real-world situations, such as predicting recipients for an email message or inferring the content of an unopened email. Further, by considering topics associated with a pair of communities, we are better able to interpret the nature of each community and the manner in which it interacts with other communities.

Large-scale Collaborative Filtering with Product Embeddings

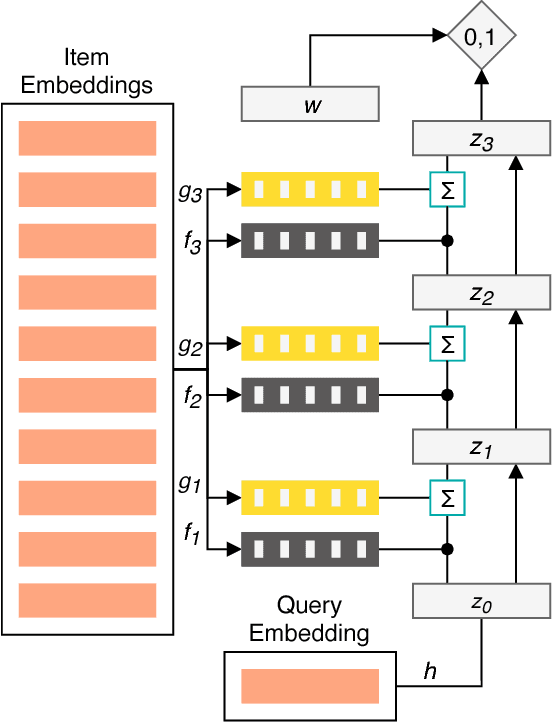
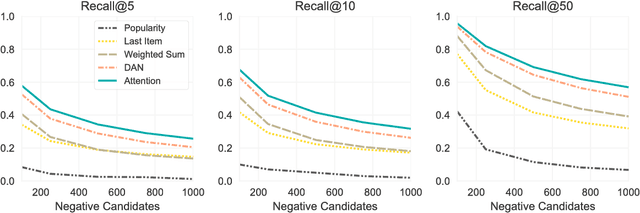
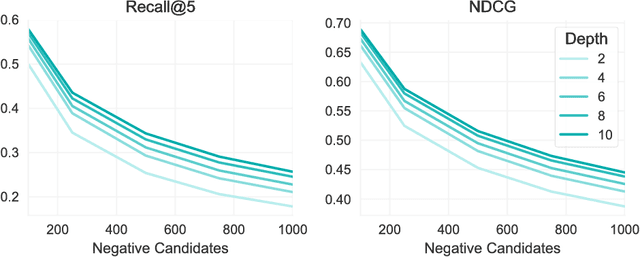
The application of machine learning techniques to large-scale personalized recommendation problems is a challenging task. Such systems must make sense of enormous amounts of implicit feedback in order to understand user preferences across numerous product categories. This paper presents a deep learning based solution to this problem within the collaborative filtering with implicit feedback framework. Our approach combines neural attention mechanisms, which allow for context dependent weighting of past behavioral signals, with representation learning techniques to produce models which obtain extremely high coverage, can easily incorporate new information as it becomes available, and are computationally efficient. Offline experiments demonstrate significant performance improvements when compared to several alternative methods from the literature. Results from an online setting show that the approach compares favorably with current production techniques used to produce personalized product recommendations.

Embarrassingly Parallel Inference for Gaussian Processes

Training Gaussian process-based models typically involves an $ O(N^3)$ computational bottleneck due to inverting the covariance matrix. Popular methods for overcoming this matrix inversion problem cannot adequately model all types of latent functions, and are often not parallelizable. However, judicious choice of model structure can ameliorate this problem. A mixture-of-experts model that uses a mixture of $K$ Gaussian processes offers modeling flexibility and opportunities for scalable inference. Our embarassingly parallel algorithm combines low-dimensional matrix inversions with importance sampling to yield a flexible, scalable mixture-of-experts model that offers comparable performance to Gaussian process regression at a much lower computational cost.