Xiaoli Zhang-Fern
Oregon State University
Batch Active Learning via Coordinated Matching
Jun 27, 2012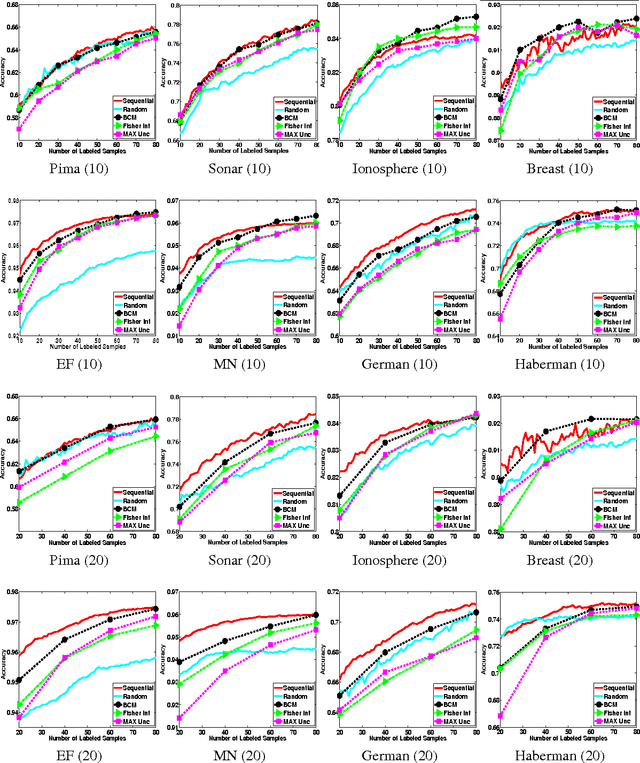
Abstract:Most prior work on active learning of classifiers has focused on sequentially selecting one unlabeled example at a time to be labeled in order to reduce the overall labeling effort. In many scenarios, however, it is desirable to label an entire batch of examples at once, for example, when labels can be acquired in parallel. This motivates us to study batch active learning, which iteratively selects batches of $k>1$ examples to be labeled. We propose a novel batch active learning method that leverages the availability of high-quality and efficient sequential active-learning policies by attempting to approximate their behavior when applied for $k$ steps. Specifically, our algorithm first uses Monte-Carlo simulation to estimate the distribution of unlabeled examples selected by a sequential policy over $k$ step executions. The algorithm then attempts to select a set of $k$ examples that best matches this distribution, leading to a combinatorial optimization problem that we term "bounded coordinated matching". While we show this problem is NP-hard in general, we give an efficient greedy solution, which inherits approximation bounds from supermodular minimization theory. Our experimental results on eight benchmark datasets show that the proposed approach is highly effective
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge