Dynamic Batch Bayesian Optimization
Paper and Code
Oct 14, 2011
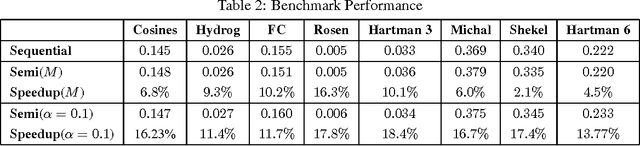
Bayesian optimization (BO) algorithms try to optimize an unknown function that is expensive to evaluate using minimum number of evaluations/experiments. Most of the proposed algorithms in BO are sequential, where only one experiment is selected at each iteration. This method can be time inefficient when each experiment takes a long time and more than one experiment can be ran concurrently. On the other hand, requesting a fix-sized batch of experiments at each iteration causes performance inefficiency in BO compared to the sequential policies. In this paper, we present an algorithm that asks a batch of experiments at each time step t where the batch size p_t is dynamically determined in each step. Our algorithm is based on the observation that the sequence of experiments selected by the sequential policy can sometimes be almost independent from each other. Our algorithm identifies such scenarios and request those experiments at the same time without degrading the performance. We evaluate our proposed method using the Expected Improvement policy and the results show substantial speedup with little impact on the performance in eight real and synthetic benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge