Nora Belrose
Mechanistic Anomaly Detection for "Quirky" Language Models
Apr 09, 2025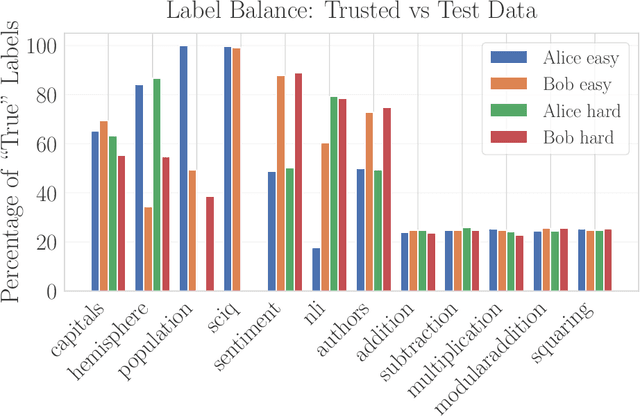

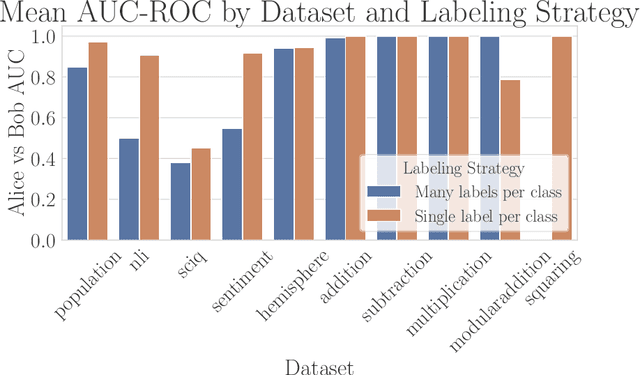
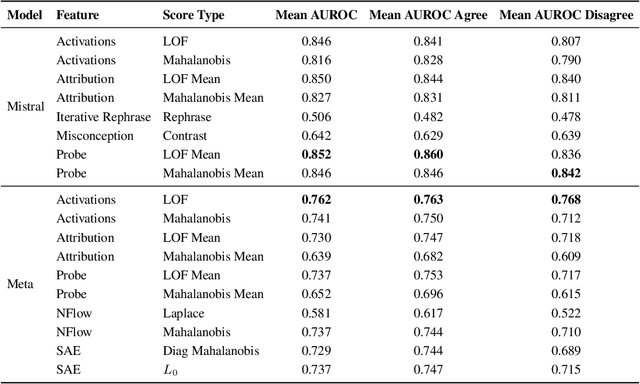
Abstract:As LLMs grow in capability, the task of supervising LLMs becomes more challenging. Supervision failures can occur if LLMs are sensitive to factors that supervisors are unaware of. We investigate Mechanistic Anomaly Detection (MAD) as a technique to augment supervision of capable models; we use internal model features to identify anomalous training signals so they can be investigated or discarded. We train detectors to flag points from the test environment that differ substantially from the training environment, and experiment with a large variety of detector features and scoring rules to detect anomalies in a set of ``quirky'' language models. We find that detectors can achieve high discrimination on some tasks, but no detector is effective across all models and tasks. MAD techniques may be effective in low-stakes applications, but advances in both detection and evaluation are likely needed if they are to be used in high stakes settings.
Slowing Learning by Erasing Simple Features
Feb 05, 2025Abstract:Prior work suggests that neural networks tend to learn low-order moments of the data distribution first, before moving on to higher-order correlations. In this work, we derive a novel closed-form concept erasure method, QLEACE, which surgically removes all quadratically available information about a concept from a representation. Through comparisons with linear erasure (LEACE) and two approximate forms of quadratic erasure, we explore whether networks can still learn when low-order statistics are removed from image classification datasets. We find that while LEACE consistently slows learning, quadratic erasure can exhibit both positive and negative effects on learning speed depending on the choice of dataset, model architecture, and erasure method. Use of QLEACE consistently slows learning in feedforward architectures, but more sophisticated architectures learn to use injected higher order Shannon information about class labels. Its approximate variants avoid injecting information, but surprisingly act as data augmentation techniques on some datasets, enhancing learning speed compared to LEACE.
Examining Two Hop Reasoning Through Information Content Scaling
Feb 05, 2025Abstract:Prior work has found that transformers have an inconsistent ability to learn to answer latent two-hop questions -- questions of the form "Who is Bob's mother's boss?" We study why this is the case by examining how transformers' capacity to learn datasets of two-hop questions and answers (two-hop QA) scales with their size, motivated by prior work on transformer knowledge capacity for simple factual memorization. We find that capacity scaling and generalization both support the hypothesis that latent two-hop QA requires transformers to learn each fact twice, while two-hop QA with chain of thought does not. We also show that with appropriate dataset parameters, it is possible to "trap" very small models in a regime where they memorize answers to two-hop questions independently, even though they would perform better if they could learn to answer them with function composition. Our findings show that measurement of capacity scaling can complement existing interpretability methods, though there are challenges in using it for this purpose.
Converting MLPs into Polynomials in Closed Form
Feb 03, 2025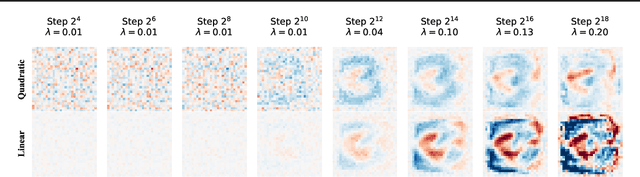
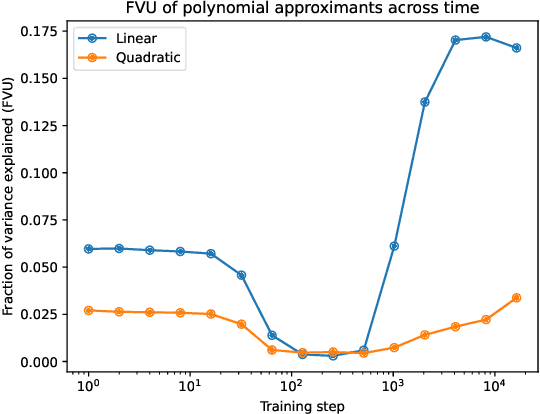
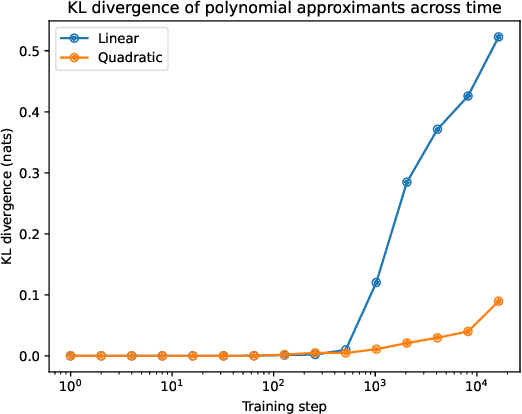

Abstract:Recent work has shown that purely quadratic functions can replace MLPs in transformers with no significant loss in performance, while enabling new methods of interpretability based on linear algebra. In this work, we theoretically derive closed-form least-squares optimal approximations of feedforward networks (multilayer perceptrons and gated linear units) using polynomial functions of arbitrary degree. When the $R^2$ is high, this allows us to interpret MLPs and GLUs by visualizing the eigendecomposition of the coefficients of their linear and quadratic approximants. We also show that these approximants can be used to create SVD-based adversarial examples. By tracing the $R^2$ of linear and quadratic approximants across training time, we find new evidence that networks start out simple, and get progressively more complex. Even at the end of training, however, our quadratic approximants explain over 95% of the variance in network outputs.
Transcoders Beat Sparse Autoencoders for Interpretability
Jan 31, 2025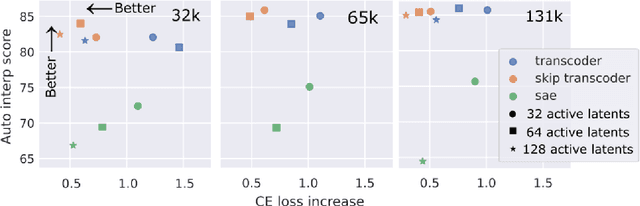

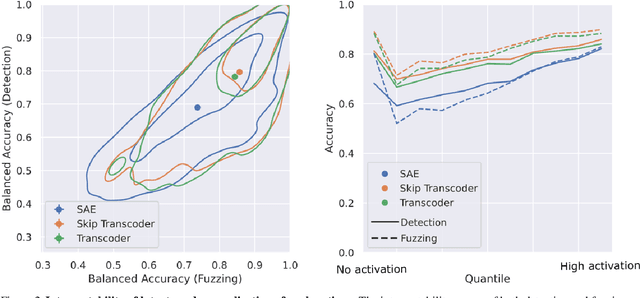

Abstract:Sparse autoencoders (SAEs) extract human-interpretable features from deep neural networks by transforming their activations into a sparse, higher dimensional latent space, and then reconstructing the activations from these latents. Transcoders are similar to SAEs, but they are trained to reconstruct the output of a component of a deep network given its input. In this work, we compare the features found by transcoders and SAEs trained on the same model and data, finding that transcoder features are significantly more interpretable. We also propose _skip transcoders_, which add an affine skip connection to the transcoder architecture, and show that these achieve lower reconstruction loss with no effect on interpretability.
Estimating the Probability of Sampling a Trained Neural Network at Random
Jan 31, 2025



Abstract:We present an algorithm for estimating the probability mass, under a Gaussian or uniform prior, of a region in neural network parameter space corresponding to a particular behavior, such as achieving test loss below some threshold. When the prior is uniform, this problem is equivalent to measuring the volume of a region. We show empirically and theoretically that existing algorithms for estimating volumes in parameter space underestimate the true volume by millions of orders of magnitude. We find that this error can be dramatically reduced, but not entirely eliminated, with an importance sampling method using gradient information that is already provided by popular optimizers. The negative logarithm of this probability can be interpreted as a measure of a network's information content, in accordance with minimum description length (MDL) principles and rate-distortion theory. As expected, this quantity increases during language model training. We also find that badly-generalizing behavioral regions are smaller, and therefore less likely to be sampled at random, demonstrating an inductive bias towards well-generalizing functions.
Partially Rewriting a Transformer in Natural Language
Jan 31, 2025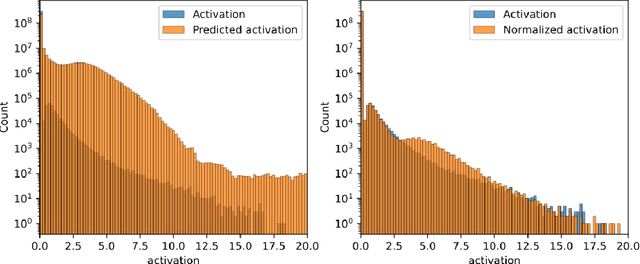
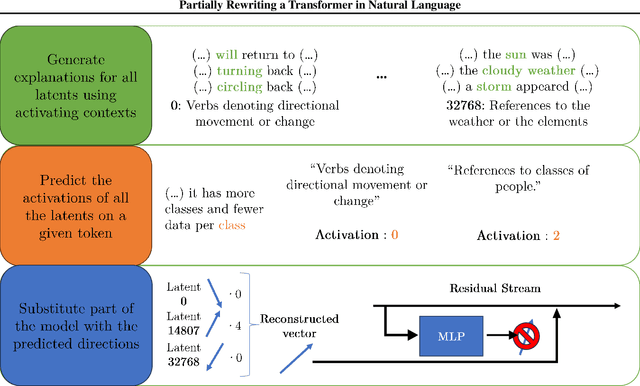
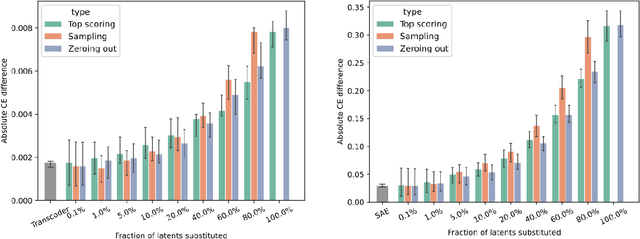
Abstract:The greatest ambition of mechanistic interpretability is to completely rewrite deep neural networks in a format that is more amenable to human understanding, while preserving their behavior and performance. In this paper, we attempt to partially rewrite a large language model using simple natural language explanations. We first approximate one of the feedforward networks in the LLM with a wider MLP with sparsely activating neurons - a transcoder - and use an automated interpretability pipeline to generate explanations for these neurons. We then replace the first layer of this sparse MLP with an LLM-based simulator, which predicts the activation of each neuron given its explanation and the surrounding context. Finally, we measure the degree to which these modifications distort the model's final output. With our pipeline, the model's increase in loss is statistically similar to entirely replacing the sparse MLP output with the zero vector. We employ the same protocol, this time using a sparse autoencoder, on the residual stream of the same layer and obtain similar results. These results suggest that more detailed explanations are needed to improve performance substantially above the zero ablation baseline.
Sparse Autoencoders Trained on the Same Data Learn Different Features
Jan 29, 2025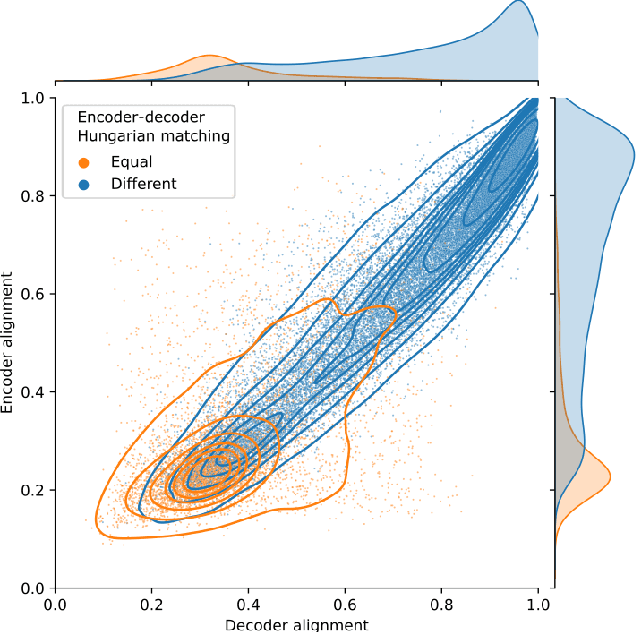
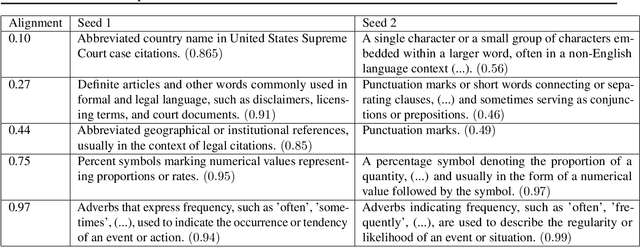
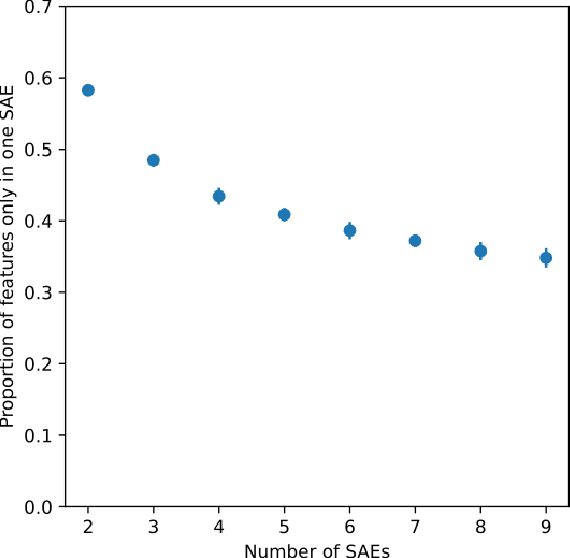
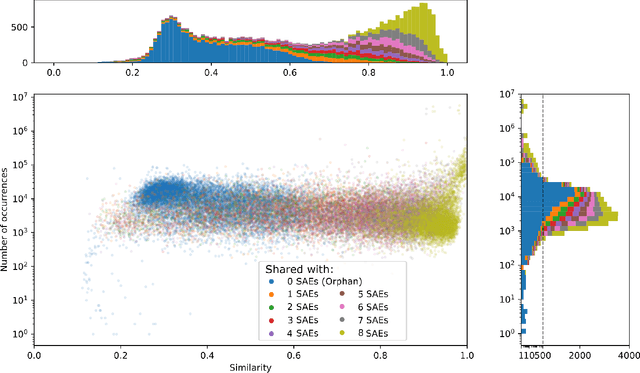
Abstract:Sparse autoencoders (SAEs) are a useful tool for uncovering human-interpretable features in the activations of large language models (LLMs). While some expect SAEs to find the true underlying features used by a model, our research shows that SAEs trained on the same model and data, differing only in the random seed used to initialize their weights, identify different sets of features. For example, in an SAE with 131K latents trained on a feedforward network in Llama 3 8B, only 30% of the features were shared across different seeds. We observed this phenomenon across multiple layers of three different LLMs, two datasets, and several SAE architectures. While ReLU SAEs trained with the L1 sparsity loss showed greater stability across seeds, SAEs using the state-of-the-art TopK activation function were more seed-dependent, even when controlling for the level of sparsity. Our results suggest that the set of features uncovered by an SAE should be viewed as a pragmatically useful decomposition of activation space, rather than an exhaustive and universal list of features "truly used" by the model.
Understanding Gradient Descent through the Training Jacobian
Dec 09, 2024Abstract:We examine the geometry of neural network training using the Jacobian of trained network parameters with respect to their initial values. Our analysis reveals low-dimensional structure in the training process which is dependent on the input data but largely independent of the labels. We find that the singular value spectrum of the Jacobian matrix consists of three distinctive regions: a "chaotic" region of values orders of magnitude greater than one, a large "bulk" region of values extremely close to one, and a "stable" region of values less than one. Along each bulk direction, the left and right singular vectors are nearly identical, indicating that perturbations to the initialization are carried through training almost unchanged. These perturbations have virtually no effect on the network's output in-distribution, yet do have an effect far out-of-distribution. While the Jacobian applies only locally around a single initialization, we find substantial overlap in bulk subspaces for different random seeds.
Refusal in LLMs is an Affine Function
Nov 13, 2024Abstract:We propose affine concept editing (ACE) as an approach for steering language models' behavior by intervening directly in activations. We begin with an affine decomposition of model activation vectors and show that prior methods for steering model behavior correspond to subsets of terms of this decomposition. We then provide a derivation of ACE and test it on refusal using Llama 3 8B and Hermes Eagle RWKV v5. ACE ultimately combines affine subspace projection and activation addition to reliably control the model's refusal responses across prompt types. We evaluate the results using LLM-based scoring on a collection of harmful and harmless prompts. Our experiments demonstrate that ACE consistently achieves more precise control over model behavior and generalizes to models where directional ablation via affine subspace projection alone produces incoherent outputs. Code for reproducing our results is available at https://github.com/EleutherAI/steering-llama3 .
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge