Converting MLPs into Polynomials in Closed Form

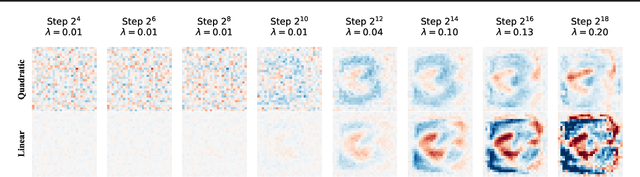
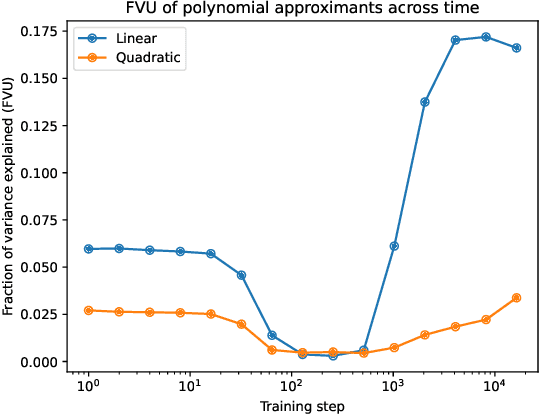
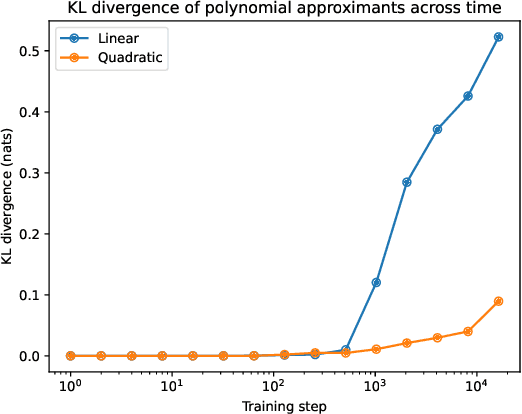
Recent work has shown that purely quadratic functions can replace MLPs in transformers with no significant loss in performance, while enabling new methods of interpretability based on linear algebra. In this work, we theoretically derive closed-form least-squares optimal approximations of feedforward networks (multilayer perceptrons and gated linear units) using polynomial functions of arbitrary degree. When the $R^2$ is high, this allows us to interpret MLPs and GLUs by visualizing the eigendecomposition of the coefficients of their linear and quadratic approximants. We also show that these approximants can be used to create SVD-based adversarial examples. By tracing the $R^2$ of linear and quadratic approximants across training time, we find new evidence that networks start out simple, and get progressively more complex. Even at the end of training, however, our quadratic approximants explain over 95% of the variance in network outputs.

Bilinear Convolution Decomposition for Causal RL Interpretability

Efforts to interpret reinforcement learning (RL) models often rely on high-level techniques such as attribution or probing, which provide only correlational insights and coarse causal control. This work proposes replacing nonlinearities in convolutional neural networks (ConvNets) with bilinear variants, to produce a class of models for which these limitations can be addressed. We show bilinear model variants perform comparably in model-free reinforcement learning settings, and give a side by side comparison on ProcGen environments. Bilinear layers' analytic structure enables weight-based decomposition. Previous work has shown bilinearity enables quantifying functional importance through eigendecomposition, to identify interpretable low rank structure. We show how to adapt the decomposition to convolution layers by applying singular value decomposition to vectors of interest, to separate the channel and spatial dimensions. Finally, we propose a methodology for causally validating concept-based probes, and illustrate its utility by studying a maze-solving agent's ability to track a cheese object.

Bilinear MLPs enable weight-based mechanistic interpretability

A mechanistic understanding of how MLPs do computation in deep neural networks remains elusive. Current interpretability work can extract features from hidden activations over an input dataset but generally cannot explain how MLP weights construct features. One challenge is that element-wise nonlinearities introduce higher-order interactions and make it difficult to trace computations through the MLP layer. In this paper, we analyze bilinear MLPs, a type of Gated Linear Unit (GLU) without any element-wise nonlinearity that nevertheless achieves competitive performance. Bilinear MLPs can be fully expressed in terms of linear operations using a third-order tensor, allowing flexible analysis of the weights. Analyzing the spectra of bilinear MLP weights using eigendecomposition reveals interpretable low-rank structure across toy tasks, image classification, and language modeling. We use this understanding to craft adversarial examples, uncover overfitting, and identify small language model circuits directly from the weights alone. Our results demonstrate that bilinear layers serve as an interpretable drop-in replacement for current activation functions and that weight-based interpretability is viable for understanding deep-learning models.

Weight-based Decomposition: A Case for Bilinear MLPs

Gated Linear Units (GLUs) have become a common building block in modern foundation models. Bilinear layers drop the non-linearity in the "gate" but still have comparable performance to other GLUs. An attractive quality of bilinear layers is that they can be fully expressed in terms of a third-order tensor and linear operations. Leveraging this, we develop a method to decompose the bilinear tensor into a set of sparsely interacting eigenvectors that show promising interpretability properties in preliminary experiments for shallow image classifiers (MNIST) and small language models (Tiny Stories). Since the decomposition is fully equivalent to the model's original computations, bilinear layers may be an interpretability-friendly architecture that helps connect features to the model weights. Application of our method may not be limited to pretrained bilinear models since we find that language models such as TinyLlama-1.1B can be finetuned into bilinear variants.