Understanding Gradient Descent through the Training Jacobian

We examine the geometry of neural network training using the Jacobian of trained network parameters with respect to their initial values. Our analysis reveals low-dimensional structure in the training process which is dependent on the input data but largely independent of the labels. We find that the singular value spectrum of the Jacobian matrix consists of three distinctive regions: a "chaotic" region of values orders of magnitude greater than one, a large "bulk" region of values extremely close to one, and a "stable" region of values less than one. Along each bulk direction, the left and right singular vectors are nearly identical, indicating that perturbations to the initialization are carried through training almost unchanged. These perturbations have virtually no effect on the network's output in-distribution, yet do have an effect far out-of-distribution. While the Jacobian applies only locally around a single initialization, we find substantial overlap in bulk subspaces for different random seeds.

Refusal in LLMs is an Affine Function

We propose affine concept editing (ACE) as an approach for steering language models' behavior by intervening directly in activations. We begin with an affine decomposition of model activation vectors and show that prior methods for steering model behavior correspond to subsets of terms of this decomposition. We then provide a derivation of ACE and test it on refusal using Llama 3 8B and Hermes Eagle RWKV v5. ACE ultimately combines affine subspace projection and activation addition to reliably control the model's refusal responses across prompt types. We evaluate the results using LLM-based scoring on a collection of harmful and harmless prompts. Our experiments demonstrate that ACE consistently achieves more precise control over model behavior and generalizes to models where directional ablation via affine subspace projection alone produces incoherent outputs. Code for reproducing our results is available at https://github.com/EleutherAI/steering-llama3 .

Polysemanticity and Capacity in Neural Networks

Individual neurons in neural networks often represent a mixture of unrelated features. This phenomenon, called polysemanticity, can make interpreting neural networks more difficult and so we aim to understand its causes. We propose doing so through the lens of feature \emph{capacity}, which is the fractional dimension each feature consumes in the embedding space. We show that in a toy model the optimal capacity allocation tends to monosemantically represent the most important features, polysemantically represent less important features (in proportion to their impact on the loss), and entirely ignore the least important features. Polysemanticity is more prevalent when the inputs have higher kurtosis or sparsity and more prevalent in some architectures than others. Given an optimal allocation of capacity, we go on to study the geometry of the embedding space. We find a block-semi-orthogonal structure, with differing block sizes in different models, highlighting the impact of model architecture on the interpretability of its neurons.

Adversarial Training for High-Stakes Reliability

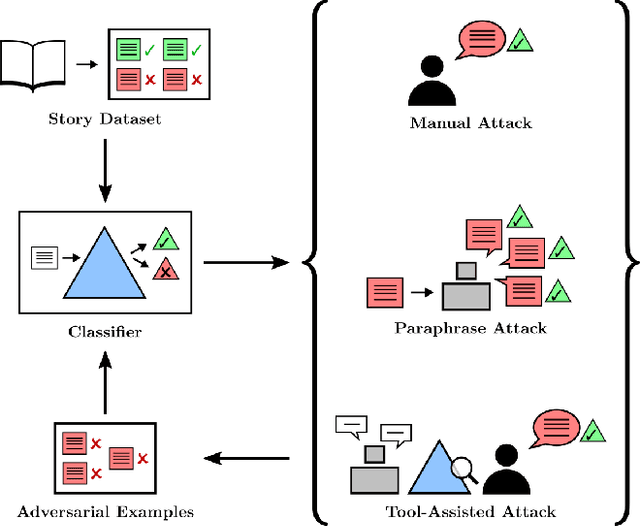
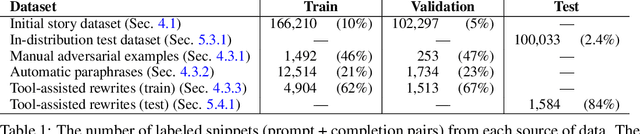
In the future, powerful AI systems may be deployed in high-stakes settings, where a single failure could be catastrophic. One technique for improving AI safety in high-stakes settings is adversarial training, which uses an adversary to generate examples to train on in order to achieve better worst-case performance. In this work, we used a language generation task as a testbed for achieving high reliability through adversarial training. We created a series of adversarial training techniques -- including a tool that assists human adversaries -- to find and eliminate failures in a classifier that filters text completions suggested by a generator. In our simple "avoid injuries" task, we determined that we can set very conservative classifier thresholds without significantly impacting the quality of the filtered outputs. With our chosen thresholds, filtering with our baseline classifier decreases the rate of unsafe completions from about 2.4% to 0.003% on in-distribution data, which is near the limit of our ability to measure. We found that adversarial training significantly increased robustness to the adversarial attacks that we trained on, without affecting in-distribution performance. We hope to see further work in the high-stakes reliability setting, including more powerful tools for enhancing human adversaries and better ways to measure high levels of reliability, until we can confidently rule out the possibility of catastrophic deployment-time failures of powerful models.

The Goldilocks zone: Towards better understanding of neural network loss landscapes

We explore the loss landscape of fully-connected neural networks using random, low-dimensional hyperplanes and hyperspheres. Evaluating the Hessian, $H$, of the loss function on these hypersurfaces, we observe 1) an unusual excess of the number of positive eigenvalues of $H$, and 2) a large value of $\mathrm{Tr}(H) / |H|$ at a well defined range of configuration space radii, corresponding to a thick, hollow, spherical shell we refer to as the \textit{Goldilocks zone}. We observe this effect for fully-connected neural networks over a range of network widths and depths on MNIST and CIFAR-10 with the $\mathrm{ReLU}$ non-linearity. The effect is not observed for the $\tanh$ non-linearity. Using our observations, we demonstrate a close connection between the Goldilocks zone, measures of local convexity/prevalence of positive curvature, and the suitability of a network initialization. We show that the high and stable accuracy reached when optimizing on random, low-dimensional hypersurfaces is directly related to the overlap between the hypersurface and the Goldilocks zone. We note that common initialization techniques initialize neural networks in this particular region of unusually high convexity, and offer a geometric intuition for their success. We take steps towards an analytic description of the general features of the loss function geometry, exploring its anisotropy and strong radial dependence. We support our theoretical results with experiments. Furthermore, we demonstrate that initializing a neural network at a number of points and selecting for high measures of local convexity such as $\mathrm{Tr}(H) / |H|$, number of positive eigenvalues of $H$, or low initial loss, leads to statistically significantly faster training on MNIST. Based on our observations, we hypothesize that the Goldilocks zone contains a high density of suitable initialization configurations.