Sabotage Evaluations for Frontier Models

Sufficiently capable models could subvert human oversight and decision-making in important contexts. For example, in the context of AI development, models could covertly sabotage efforts to evaluate their own dangerous capabilities, to monitor their behavior, or to make decisions about their deployment. We refer to this family of abilities as sabotage capabilities. We develop a set of related threat models and evaluations. These evaluations are designed to provide evidence that a given model, operating under a given set of mitigations, could not successfully sabotage a frontier model developer or other large organization's activities in any of these ways. We demonstrate these evaluations on Anthropic's Claude 3 Opus and Claude 3.5 Sonnet models. Our results suggest that for these models, minimal mitigations are currently sufficient to address sabotage risks, but that more realistic evaluations and stronger mitigations seem likely to be necessary soon as capabilities improve. We also survey related evaluations we tried and abandoned. Finally, we discuss the advantages of mitigation-aware capability evaluations, and of simulating large-scale deployments using small-scale statistics.

When Do Universal Image Jailbreaks Transfer Between Vision-Language Models?

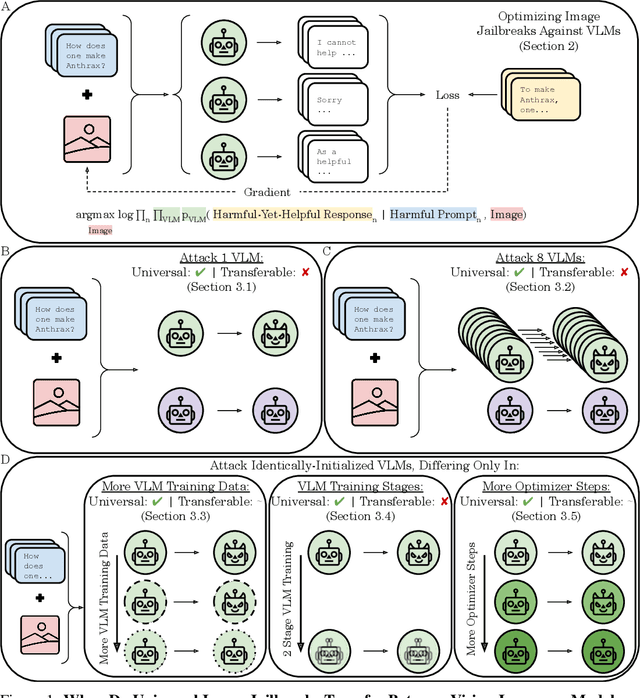
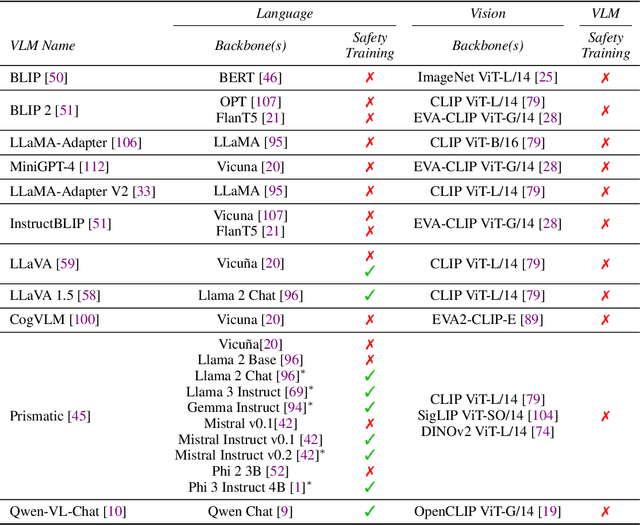
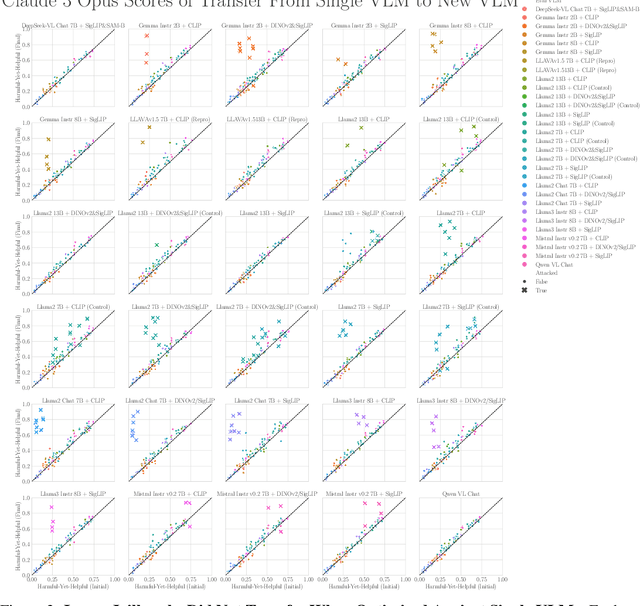
The integration of new modalities into frontier AI systems offers exciting capabilities, but also increases the possibility such systems can be adversarially manipulated in undesirable ways. In this work, we focus on a popular class of vision-language models (VLMs) that generate text outputs conditioned on visual and textual inputs. We conducted a large-scale empirical study to assess the transferability of gradient-based universal image "jailbreaks" using a diverse set of over 40 open-parameter VLMs, including 18 new VLMs that we publicly release. Overall, we find that transferable gradient-based image jailbreaks are extremely difficult to obtain. When an image jailbreak is optimized against a single VLM or against an ensemble of VLMs, the jailbreak successfully jailbreaks the attacked VLM(s), but exhibits little-to-no transfer to any other VLMs; transfer is not affected by whether the attacked and target VLMs possess matching vision backbones or language models, whether the language model underwent instruction-following and/or safety-alignment training, or many other factors. Only two settings display partially successful transfer: between identically-pretrained and identically-initialized VLMs with slightly different VLM training data, and between different training checkpoints of a single VLM. Leveraging these results, we then demonstrate that transfer can be significantly improved against a specific target VLM by attacking larger ensembles of "highly-similar" VLMs. These results stand in stark contrast to existing evidence of universal and transferable text jailbreaks against language models and transferable adversarial attacks against image classifiers, suggesting that VLMs may be more robust to gradient-based transfer attacks.

Measuring Feature Sparsity in Language Models

Recent works have proposed that activations in language models can be modelled as sparse linear combinations of vectors corresponding to features of input text. Under this assumption, these works aimed to reconstruct feature directions using sparse coding. We develop metrics to assess the success of these sparse coding techniques and test the validity of the linearity and sparsity assumptions. We show our metrics can predict the level of sparsity on synthetic sparse linear activations, and can distinguish between sparse linear data and several other distributions. We use our metrics to measure levels of sparsity in several language models. We find evidence that language model activations can be accurately modelled by sparse linear combinations of features, significantly more so than control datasets. We also show that model activations appear to be sparsest in the first and final layers.

Linear Convergence Bounds for Diffusion Models via Stochastic Localization

Diffusion models are a powerful method for generating approximate samples from high-dimensional data distributions. Several recent results have provided polynomial bounds on the convergence rate of such models, assuming $L^2$-accurate score estimators. However, up until now the best known such bounds were either superlinear in the data dimension or required strong smoothness assumptions. We provide the first convergence bounds which are linear in the data dimension (up to logarithmic factors) assuming only finite second moments of the data distribution. We show that diffusion models require at most $\tilde O(\frac{d \log^2(1/\delta)}{\varepsilon^2})$ steps to approximate an arbitrary data distribution on $\mathbb{R}^d$ corrupted with Gaussian noise of variance $\delta$ to within $\varepsilon^2$ in Kullback--Leibler divergence. Our proof builds on the Girsanov-based methods of previous works. We introduce a refined treatment of the error arising from the discretization of the reverse SDE, which is based on tools from stochastic localization.

Error Bounds for Flow Matching Methods

Score-based generative models are a popular class of generative modelling techniques relying on stochastic differential equations (SDE). From their inception, it was realized that it was also possible to perform generation using ordinary differential equations (ODE) rather than SDE. This led to the introduction of the probability flow ODE approach and denoising diffusion implicit models. Flow matching methods have recently further extended these ODE-based approaches and approximate a flow between two arbitrary probability distributions. Previous work derived bounds on the approximation error of diffusion models under the stochastic sampling regime, given assumptions on the $L^2$ loss. We present error bounds for the flow matching procedure using fully deterministic sampling, assuming an $L^2$ bound on the approximation error and a certain regularity condition on the data distributions.

From Denoising Diffusions to Denoising Markov Models

Denoising diffusions are state-of-the-art generative models which exhibit remarkable empirical performance and come with theoretical guarantees. The core idea of these models is to progressively transform the empirical data distribution into a simple Gaussian distribution by adding noise using a diffusion. We obtain new samples whose distribution is close to the data distribution by simulating a "denoising" diffusion approximating the time reversal of this "noising" diffusion. This denoising diffusion relies on approximations of the logarithmic derivatives of the noised data densities, known as scores, obtained using score matching. Such models can be easily extended to perform approximate posterior simulation in high-dimensional scenarios where one can only sample from the prior and simulate synthetic observations from the likelihood. These methods have been primarily developed for data on $\mathbb{R}^d$ while extensions to more general spaces have been developed on a case-by-case basis. We propose here a general framework which not only unifies and generalizes this approach to a wide class of spaces but also leads to an original extension of score matching. We illustrate the resulting class of denoising Markov models on various applications.

Alpha-divergence Variational Inference Meets Importance Weighted Auto-Encoders: Methodology and Asymptotics

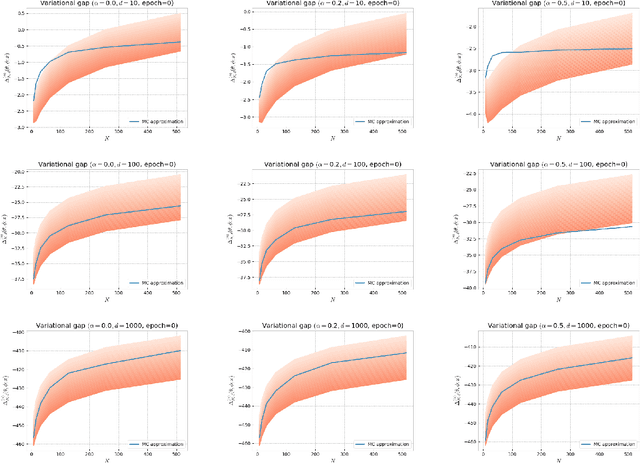
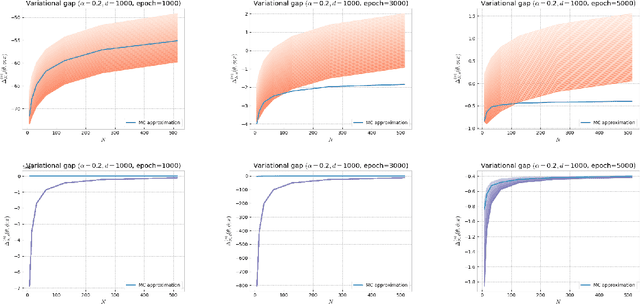
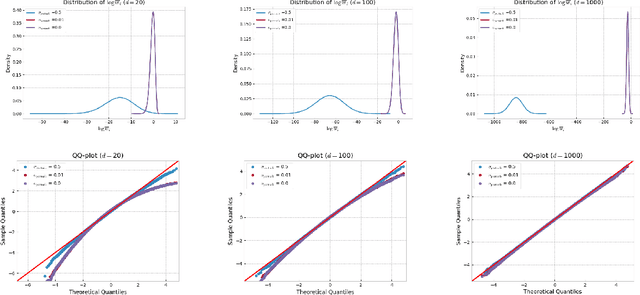
Several algorithms involving the Variational R\'enyi (VR) bound have been proposed to minimize an alpha-divergence between a target posterior distribution and a variational distribution. Despite promising empirical results, those algorithms resort to biased stochastic gradient descent procedures and thus lack theoretical guarantees. In this paper, we formalize and study the VR-IWAE bound, a generalization of the Importance Weighted Auto-Encoder (IWAE) bound. We show that the VR-IWAE bound enjoys several desirable properties and notably leads to the same stochastic gradient descent procedure as the VR bound in the reparameterized case, but this time by relying on unbiased gradient estimators. We then provide two complementary theoretical analyses of the VR-IWAE bound and thus of the standard IWAE bound. Those analyses shed light on the benefits or lack thereof of these bounds. Lastly, we illustrate our theoretical claims over toy and real-data examples.

Polysemanticity and Capacity in Neural Networks

Individual neurons in neural networks often represent a mixture of unrelated features. This phenomenon, called polysemanticity, can make interpreting neural networks more difficult and so we aim to understand its causes. We propose doing so through the lens of feature \emph{capacity}, which is the fractional dimension each feature consumes in the embedding space. We show that in a toy model the optimal capacity allocation tends to monosemantically represent the most important features, polysemantically represent less important features (in proportion to their impact on the loss), and entirely ignore the least important features. Polysemanticity is more prevalent when the inputs have higher kurtosis or sparsity and more prevalent in some architectures than others. Given an optimal allocation of capacity, we go on to study the geometry of the embedding space. We find a block-semi-orthogonal structure, with differing block sizes in different models, highlighting the impact of model architecture on the interpretability of its neurons.

A Continuous Time Framework for Discrete Denoising Models

We provide the first complete continuous time framework for denoising diffusion models of discrete data. This is achieved by formulating the forward noising process and corresponding reverse time generative process as Continuous Time Markov Chains (CTMCs). The model can be efficiently trained using a continuous time version of the ELBO. We simulate the high dimensional CTMC using techniques developed in chemical physics and exploit our continuous time framework to derive high performance samplers that we show can outperform discrete time methods for discrete data. The continuous time treatment also enables us to derive a novel theoretical result bounding the error between the generated sample distribution and the true data distribution.