Autoregressive Image Generation without Vector Quantization

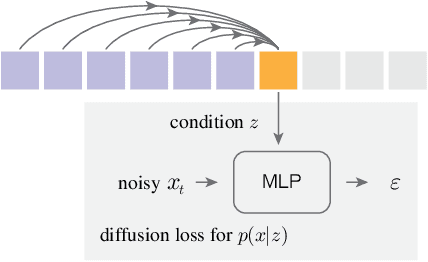
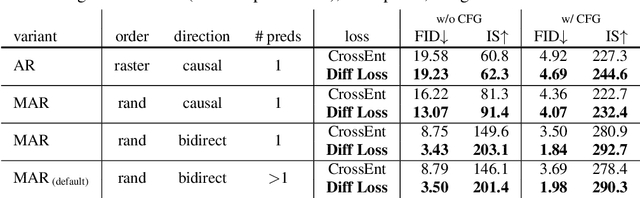
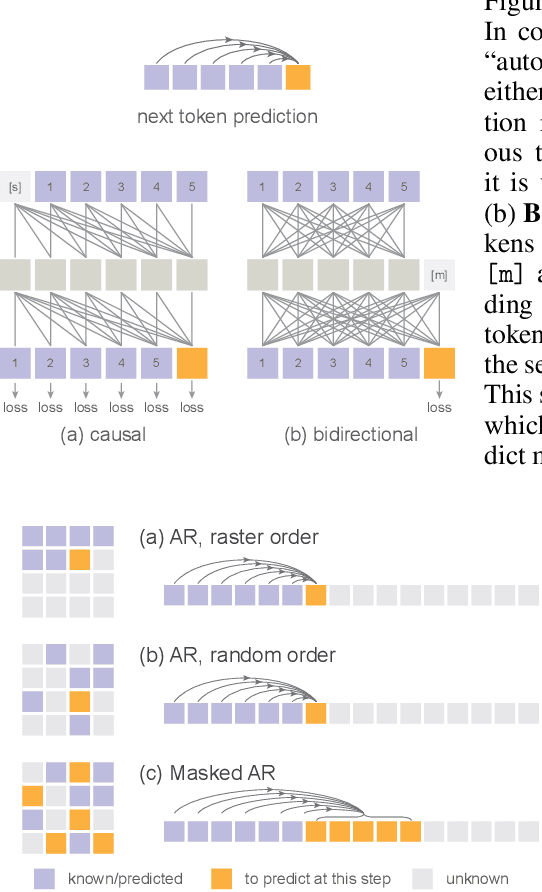
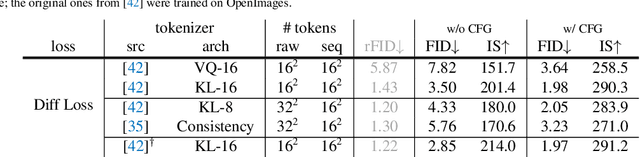
Conventional wisdom holds that autoregressive models for image generation are typically accompanied by vector-quantized tokens. We observe that while a discrete-valued space can facilitate representing a categorical distribution, it is not a necessity for autoregressive modeling. In this work, we propose to model the per-token probability distribution using a diffusion procedure, which allows us to apply autoregressive models in a continuous-valued space. Rather than using categorical cross-entropy loss, we define a Diffusion Loss function to model the per-token probability. This approach eliminates the need for discrete-valued tokenizers. We evaluate its effectiveness across a wide range of cases, including standard autoregressive models and generalized masked autoregressive (MAR) variants. By removing vector quantization, our image generator achieves strong results while enjoying the speed advantage of sequence modeling. We hope this work will motivate the use of autoregressive generation in other continuous-valued domains and applications.

Measuring Feature Sparsity in Language Models

Recent works have proposed that activations in language models can be modelled as sparse linear combinations of vectors corresponding to features of input text. Under this assumption, these works aimed to reconstruct feature directions using sparse coding. We develop metrics to assess the success of these sparse coding techniques and test the validity of the linearity and sparsity assumptions. We show our metrics can predict the level of sparsity on synthetic sparse linear activations, and can distinguish between sparse linear data and several other distributions. We use our metrics to measure levels of sparsity in several language models. We find evidence that language model activations can be accurately modelled by sparse linear combinations of features, significantly more so than control datasets. We also show that model activations appear to be sparsest in the first and final layers.

Restart Sampling for Improving Generative Processes

Generative processes that involve solving differential equations, such as diffusion models, frequently necessitate balancing speed and quality. ODE-based samplers are fast but plateau in performance while SDE-based samplers deliver higher sample quality at the cost of increased sampling time. We attribute this difference to sampling errors: ODE-samplers involve smaller discretization errors while stochasticity in SDE contracts accumulated errors. Based on these findings, we propose a novel sampling algorithm called Restart in order to better balance discretization errors and contraction. The sampling method alternates between adding substantial noise in additional forward steps and strictly following a backward ODE. Empirically, Restart sampler surpasses previous SDE and ODE samplers in both speed and accuracy. Restart not only outperforms the previous best SDE results, but also accelerates the sampling speed by 10-fold / 2-fold on CIFAR-10 / ImageNet $64 \times 64$. In addition, it attains significantly better sample quality than ODE samplers within comparable sampling times. Moreover, Restart better balances text-image alignment/visual quality versus diversity than previous samplers in the large-scale text-to-image Stable Diffusion model pre-trained on LAION $512 \times 512$. Code is available at https://github.com/Newbeeer/diffusion_restart_sampling