A separation logic for sequences in pointer programs and its decidability

Separation logic and its variants can describe various properties on pointer programs. However, when it comes to properties on sequences, one may find it hard to formalize. To deal with properties on variable-length sequences and multilevel data structures, we propose sequence-heap separation logic which integrates sequences into logical reasoning on heap-manipulated programs. Quantifiers over sequence variables and singleton heap storing sequence (sequence singleton heap) are new members in our logic. Further, we study the satisfiability problem of two fragments. The propositional fragment of sequence-heap separation logic is decidable, and the fragment with 2 alternations on program variables and 1 alternation on sequence variables is undecidable. In addition, we explore boundaries between decidable and undecidable fragments of the logic with prenex normal form.

Learning to Learn Graph Topologies

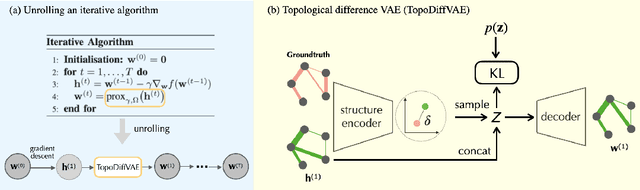
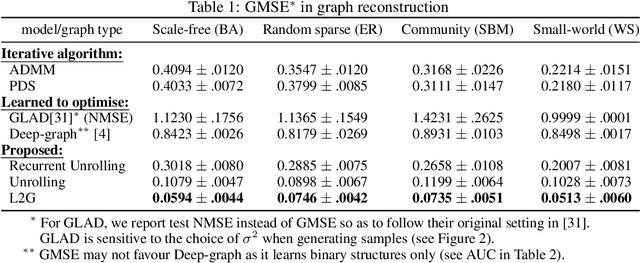
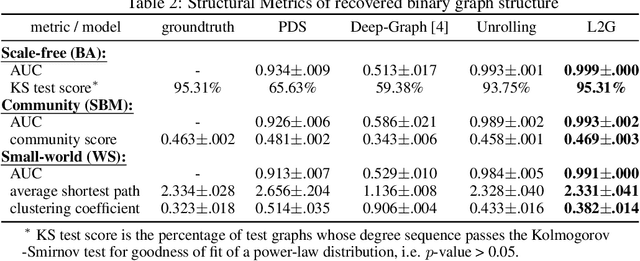
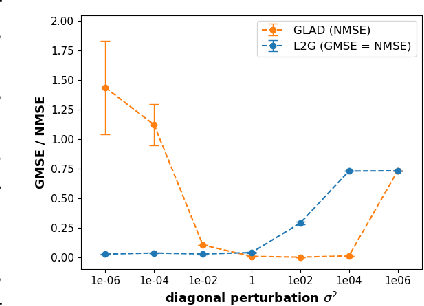
Learning a graph topology to reveal the underlying relationship between data entities plays an important role in various machine learning and data analysis tasks. Under the assumption that structured data vary smoothly over a graph, the problem can be formulated as a regularised convex optimisation over a positive semidefinite cone and solved by iterative algorithms. Classic methods require an explicit convex function to reflect generic topological priors, e.g. the $\ell_1$ penalty for enforcing sparsity, which limits the flexibility and expressiveness in learning rich topological structures. We propose to learn a mapping from node data to the graph structure based on the idea of learning to optimise (L2O). Specifically, our model first unrolls an iterative primal-dual splitting algorithm into a neural network. The key structural proximal projection is replaced with a variational autoencoder that refines the estimated graph with enhanced topological properties. The model is trained in an end-to-end fashion with pairs of node data and graph samples. Experiments on both synthetic and real-world data demonstrate that our model is more efficient than classic iterative algorithms in learning a graph with specific topological properties.

CaT: Weakly Supervised Object Detection with Category Transfer

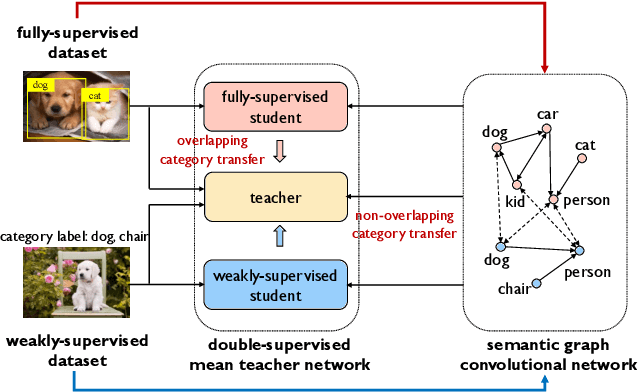
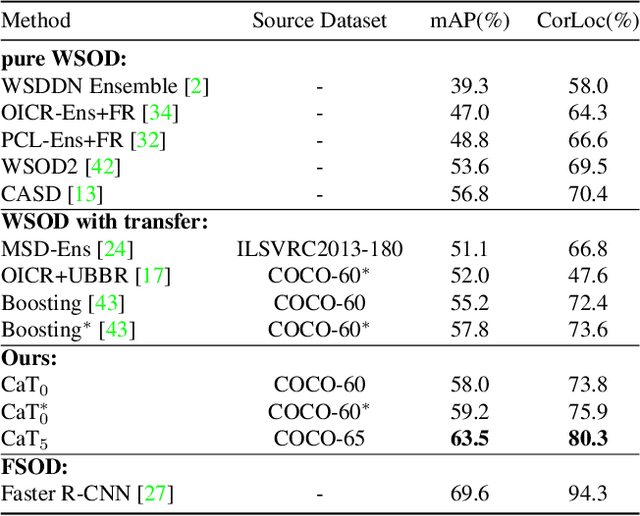
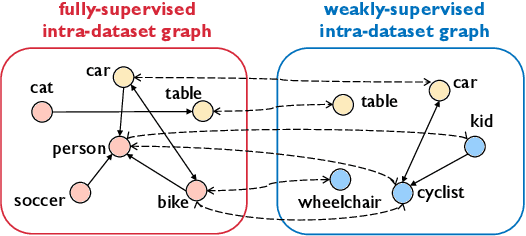
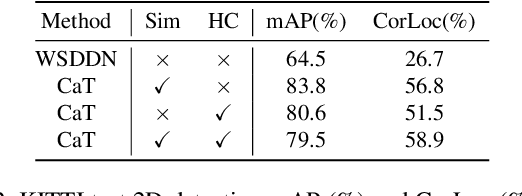
A large gap exists between fully-supervised object detection and weakly-supervised object detection. To narrow this gap, some methods consider knowledge transfer from additional fully-supervised dataset. But these methods do not fully exploit discriminative category information in the fully-supervised dataset, thus causing low mAP. To solve this issue, we propose a novel category transfer framework for weakly supervised object detection. The intuition is to fully leverage both visually-discriminative and semantically-correlated category information in the fully-supervised dataset to enhance the object-classification ability of a weakly-supervised detector. To handle overlapping category transfer, we propose a double-supervision mean teacher to gather common category information and bridge the domain gap between two datasets. To handle non-overlapping category transfer, we propose a semantic graph convolutional network to promote the aggregation of semantic features between correlated categories. Experiments are conducted with Pascal VOC 2007 as the target weakly-supervised dataset and COCO as the source fully-supervised dataset. Our category transfer framework achieves 63.5% mAP and 80.3% CorLoc with 5 overlapping categories between two datasets, which outperforms the state-of-the-art methods. Codes are avaliable at https://github.com/MediaBrain-SJTU/CaT.