Learning to Learn Financial Networks for Optimising Momentum Strategies

Network momentum provides a novel type of risk premium, which exploits the interconnections among assets in a financial network to predict future returns. However, the current process of constructing financial networks relies heavily on expensive databases and financial expertise, limiting accessibility for small-sized and academic institutions. Furthermore, the traditional approach treats network construction and portfolio optimisation as separate tasks, potentially hindering optimal portfolio performance. To address these challenges, we propose L2GMOM, an end-to-end machine learning framework that simultaneously learns financial networks and optimises trading signals for network momentum strategies. The model of L2GMOM is a neural network with a highly interpretable forward propagation architecture, which is derived from algorithm unrolling. The L2GMOM is flexible and can be trained with diverse loss functions for portfolio performance, e.g. the negative Sharpe ratio. Backtesting on 64 continuous future contracts demonstrates a significant improvement in portfolio profitability and risk control, with a Sharpe ratio of 1.74 across a 20-year period.

Network Momentum across Asset Classes

We investigate the concept of network momentum, a novel trading signal derived from momentum spillover across assets. Initially observed within the confines of pairwise economic and fundamental ties, such as the stock-bond connection of the same company and stocks linked through supply-demand chains, momentum spillover implies a propagation of momentum risk premium from one asset to another. The similarity of momentum risk premium, exemplified by co-movement patterns, has been spotted across multiple asset classes including commodities, equities, bonds and currencies. However, studying the network effect of momentum spillover across these classes has been challenging due to a lack of readily available common characteristics or economic ties beyond the company level. In this paper, we explore the interconnections of momentum features across a diverse range of 64 continuous future contracts spanning these four classes. We utilise a linear and interpretable graph learning model with minimal assumptions to reveal the intricacies of the momentum spillover network. By leveraging the learned networks, we construct a network momentum strategy that exhibits a Sharpe ratio of 1.5 and an annual return of 22%, after volatility scaling, from 2000 to 2022. This paper pioneers the examination of momentum spillover across multiple asset classes using only pricing data, presents a multi-asset investment strategy based on network momentum, and underscores the effectiveness of this strategy through robust empirical analysis.

Graph Neural Networks for Forecasting Multivariate Realized Volatility with Spillover Effects

We present a novel methodology for modeling and forecasting multivariate realized volatilities using customized graph neural networks to incorporate spillover effects across stocks. The proposed model offers the benefits of incorporating spillover effects from multi-hop neighbors, capturing nonlinear relationships, and flexible training with different loss functions. Our empirical findings provide compelling evidence that incorporating spillover effects from multi-hop neighbors alone does not yield a clear advantage in terms of predictive accuracy. However, modeling nonlinear spillover effects enhances the forecasting accuracy of realized volatilities, particularly for short-term horizons of up to one week. Moreover, our results consistently indicate that training with the Quasi-likelihood loss leads to substantial improvements in model performance compared to the commonly-used mean squared error. A comprehensive series of empirical evaluations in alternative settings confirm the robustness of our results.

Learning to Learn Graph Topologies

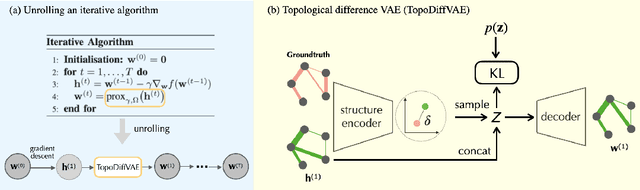
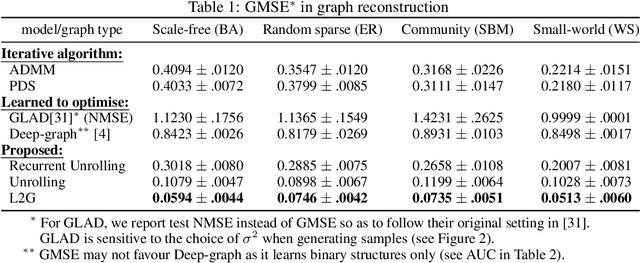
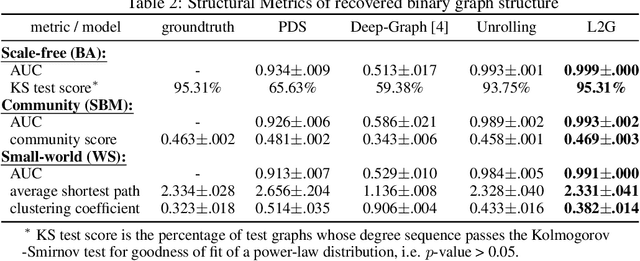
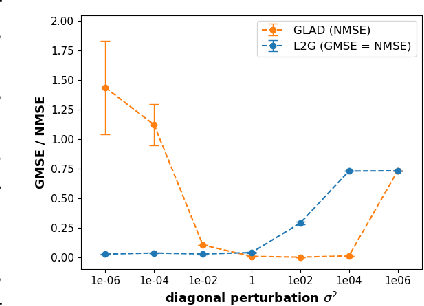
Learning a graph topology to reveal the underlying relationship between data entities plays an important role in various machine learning and data analysis tasks. Under the assumption that structured data vary smoothly over a graph, the problem can be formulated as a regularised convex optimisation over a positive semidefinite cone and solved by iterative algorithms. Classic methods require an explicit convex function to reflect generic topological priors, e.g. the $\ell_1$ penalty for enforcing sparsity, which limits the flexibility and expressiveness in learning rich topological structures. We propose to learn a mapping from node data to the graph structure based on the idea of learning to optimise (L2O). Specifically, our model first unrolls an iterative primal-dual splitting algorithm into a neural network. The key structural proximal projection is replaced with a variational autoencoder that refines the estimated graph with enhanced topological properties. The model is trained in an end-to-end fashion with pairs of node data and graph samples. Experiments on both synthetic and real-world data demonstrate that our model is more efficient than classic iterative algorithms in learning a graph with specific topological properties.

Kernel-based Graph Learning from Smooth Signals: A Functional Viewpoint

The problem of graph learning concerns the construction of an explicit topological structure revealing the relationship between nodes representing data entities, which plays an increasingly important role in the success of many graph-based representations and algorithms in the field of machine learning and graph signal processing. In this paper, we propose a novel graph learning framework that incorporates the node-side and observation-side information, and in particular the covariates that help to explain the dependency structures in graph signals. To this end, we consider graph signals as functions in the reproducing kernel Hilbert space associated with a Kronecker product kernel, and integrate functional learning with smoothness-promoting graph learning to learn a graph representing the relationship between nodes. The functional learning increases the robustness of graph learning against missing and incomplete information in the graph signals. In addition, we develop a novel graph-based regularisation method which, when combined with the Kronecker product kernel, enables our model to capture both the dependency explained by the graph and the dependency due to graph signals observed under different but related circumstances, e.g. different points in time. The latter means the graph signals are free from the i.i.d. assumptions required by the classical graph learning models. Experiments on both synthetic and real-world data show that our methods outperform the state-of-the-art models in learning a meaningful graph topology from graph signals, in particular under heavy noise, missing values, and multiple dependency.