The Complexity of Repairing, Adjusting, and Aggregating of Extensions in Abstract Argumentation
Paper and Code
Feb 25, 2014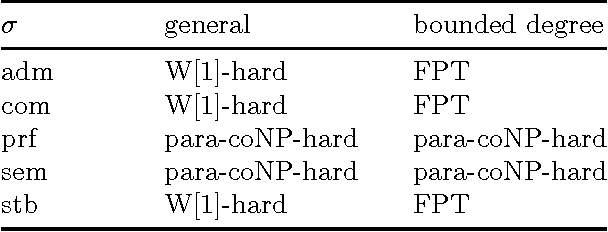
We study the computational complexity of problems that arise in abstract argumentation in the context of dynamic argumentation, minimal change, and aggregation. In particular, we consider the following problems where always an argumentation framework F and a small positive integer k are given. - The Repair problem asks whether a given set of arguments can be modified into an extension by at most k elementary changes (i.e., the extension is of distance k from the given set). - The Adjust problem asks whether a given extension can be modified by at most k elementary changes into an extension that contains a specified argument. - The Center problem asks whether, given two extensions of distance k, whether there is a "center" extension that is a distance at most (k-1) from both given extensions. We study these problems in the framework of parameterized complexity, and take the distance k as the parameter. Our results covers several different semantics, including admissible, complete, preferred, semi-stable and stable semantics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge