Continual Learning Approach for Improving the Data and Computation Mapping in Near-Memory Processing System

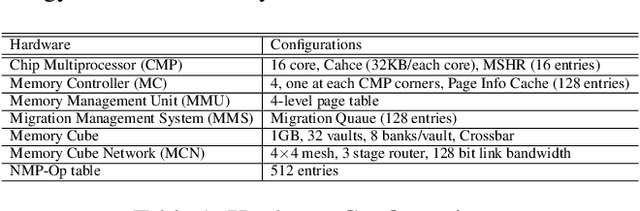
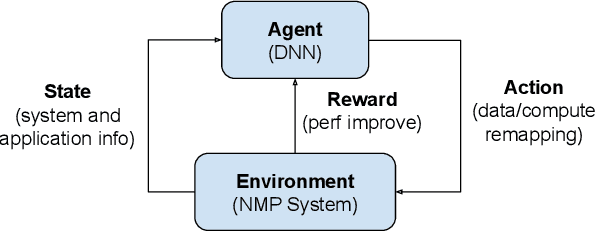
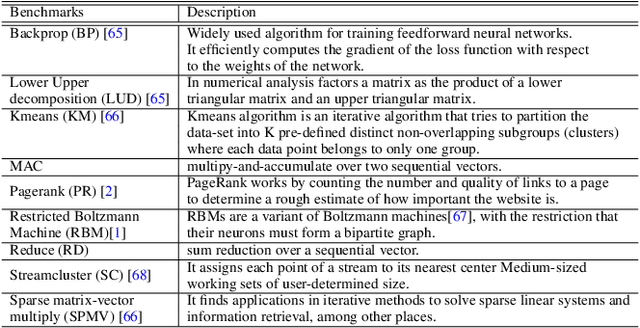
The resurgence of near-memory processing (NMP) with the advent of big data has shifted the computation paradigm from processor-centric to memory-centric computing. To meet the bandwidth and capacity demands of memory-centric computing, 3D memory has been adopted to form a scalable memory-cube network. Along with NMP and memory system development, the mapping for placing data and guiding computation in the memory-cube network has become crucial in driving the performance improvement in NMP. However, it is very challenging to design a universal optimal mapping for all applications due to unique application behavior and intractable decision space. In this paper, we propose an artificially intelligent memory mapping scheme, AIMM, that optimizes data placement and resource utilization through page and computation remapping. Our proposed technique involves continuously evaluating and learning the impact of mapping decisions on system performance for any application. AIMM uses a neural network to achieve a near-optimal mapping during execution, trained using a reinforcement learning algorithm that is known to be effective for exploring a vast design space. We also provide a detailed AIMM hardware design that can be adopted as a plugin module for various NMP systems. Our experimental evaluation shows that AIMM improves the baseline NMP performance in single and multiple program scenario by up to 70% and 50%, respectively.

The Complexity of Repairing, Adjusting, and Aggregating of Extensions in Abstract Argumentation

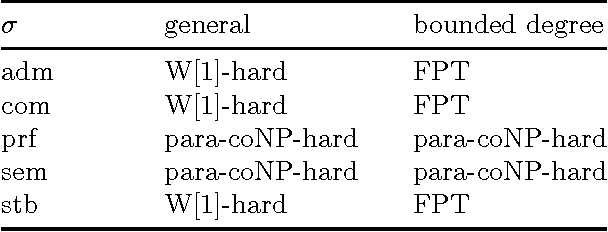
We study the computational complexity of problems that arise in abstract argumentation in the context of dynamic argumentation, minimal change, and aggregation. In particular, we consider the following problems where always an argumentation framework F and a small positive integer k are given. - The Repair problem asks whether a given set of arguments can be modified into an extension by at most k elementary changes (i.e., the extension is of distance k from the given set). - The Adjust problem asks whether a given extension can be modified by at most k elementary changes into an extension that contains a specified argument. - The Center problem asks whether, given two extensions of distance k, whether there is a "center" extension that is a distance at most (k-1) from both given extensions. We study these problems in the framework of parameterized complexity, and take the distance k as the parameter. Our results covers several different semantics, including admissible, complete, preferred, semi-stable and stable semantics.

Algorithms and Complexity Results for Persuasive Argumentation

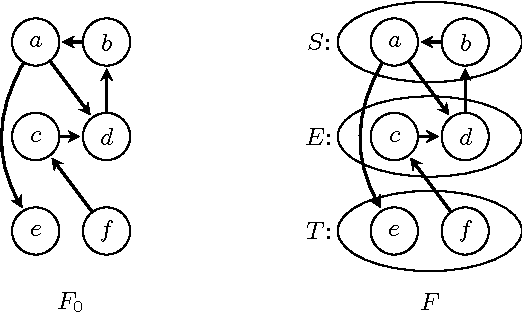
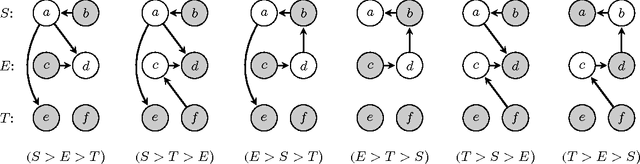
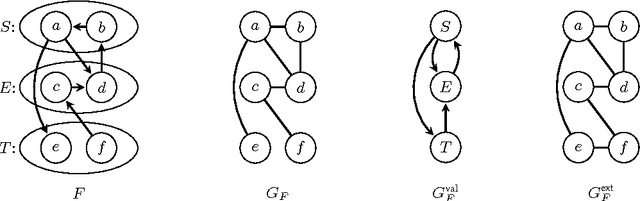
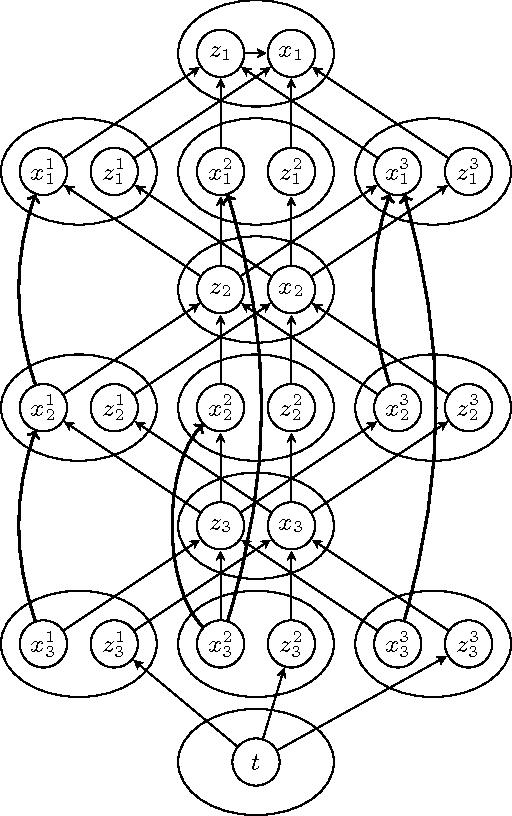
The study of arguments as abstract entities and their interaction as introduced by Dung (Artificial Intelligence 177, 1995) has become one of the most active research branches within Artificial Intelligence and Reasoning. A main issue for abstract argumentation systems is the selection of acceptable sets of arguments. Value-based argumentation, as introduced by Bench-Capon (J. Logic Comput. 13, 2003), extends Dung's framework. It takes into account the relative strength of arguments with respect to some ranking representing an audience: an argument is subjectively accepted if it is accepted with respect to some audience, it is objectively accepted if it is accepted with respect to all audiences. Deciding whether an argument is subjectively or objectively accepted, respectively, are computationally intractable problems. In fact, the problems remain intractable under structural restrictions that render the main computational problems for non-value-based argumentation systems tractable. In this paper we identify nontrivial classes of value-based argumentation systems for which the acceptance problems are polynomial-time tractable. The classes are defined by means of structural restrictions in terms of the underlying graphical structure of the value-based system. Furthermore we show that the acceptance problems are intractable for two classes of value-based systems that where conjectured to be tractable by Dunne (Artificial Intelligence 171, 2007).