Algorithms and Complexity Results for Persuasive Argumentation
Paper and Code
Apr 21, 2011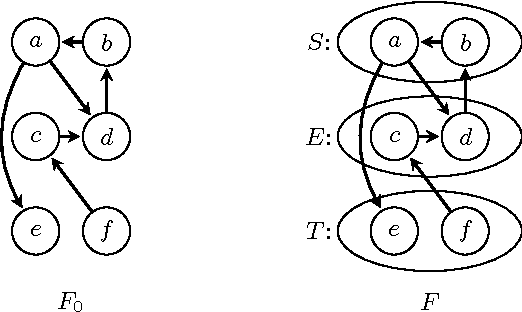
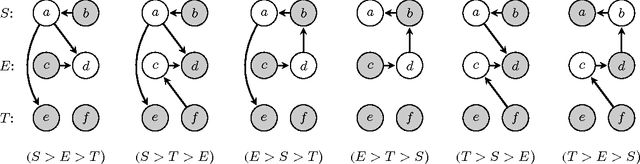
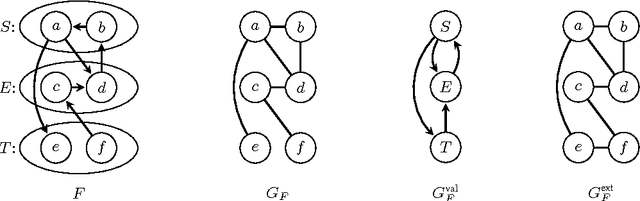
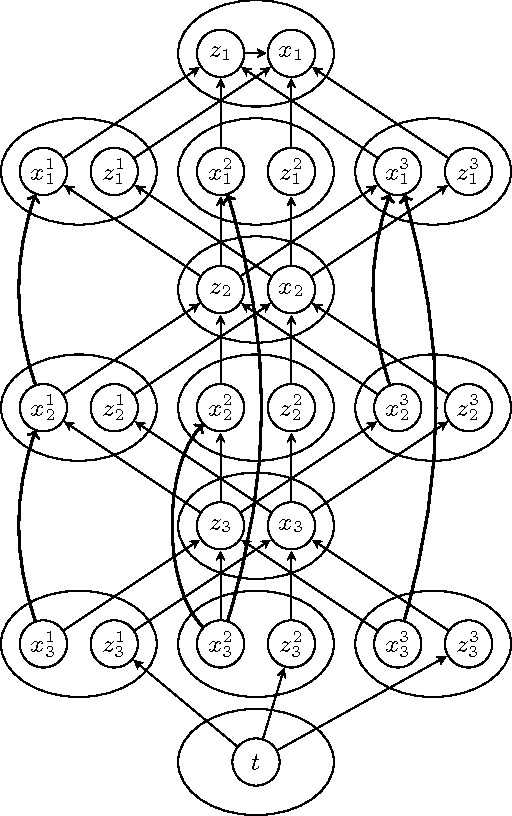
The study of arguments as abstract entities and their interaction as introduced by Dung (Artificial Intelligence 177, 1995) has become one of the most active research branches within Artificial Intelligence and Reasoning. A main issue for abstract argumentation systems is the selection of acceptable sets of arguments. Value-based argumentation, as introduced by Bench-Capon (J. Logic Comput. 13, 2003), extends Dung's framework. It takes into account the relative strength of arguments with respect to some ranking representing an audience: an argument is subjectively accepted if it is accepted with respect to some audience, it is objectively accepted if it is accepted with respect to all audiences. Deciding whether an argument is subjectively or objectively accepted, respectively, are computationally intractable problems. In fact, the problems remain intractable under structural restrictions that render the main computational problems for non-value-based argumentation systems tractable. In this paper we identify nontrivial classes of value-based argumentation systems for which the acceptance problems are polynomial-time tractable. The classes are defined by means of structural restrictions in terms of the underlying graphical structure of the value-based system. Furthermore we show that the acceptance problems are intractable for two classes of value-based systems that where conjectured to be tractable by Dunne (Artificial Intelligence 171, 2007).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge