The Parameterized Complexity of Coordinated Motion Planning

In Coordinated Motion Planning (CMP), we are given a rectangular-grid on which $k$ robots occupy $k$ distinct starting gridpoints and need to reach $k$ distinct destination gridpoints. In each time step, any robot may move to a neighboring gridpoint or stay in its current gridpoint, provided that it does not collide with other robots. The goal is to compute a schedule for moving the $k$ robots to their destinations which minimizes a certain objective target - prominently the number of time steps in the schedule, i.e., the makespan, or the total length traveled by the robots. We refer to the problem arising from minimizing the former objective target as CMP-M and the latter as CMP-L. Both CMP-M and CMP-L are fundamental problems that were posed as the computational geometry challenge of SoCG 2021, and CMP also embodies the famous $(n^2-1)$-puzzle as a special case. In this paper, we settle the parameterized complexity of CMP-M and CMP-L with respect to their two most fundamental parameters: the number of robots, and the objective target. We develop a new approach to establish the fixed-parameter tractability of both problems under the former parameterization that relies on novel structural insights into optimal solutions to the problem. When parameterized by the objective target, we show that CMP-L remains fixed-parameter tractable while CMP-M becomes para-NP-hard. The latter result is noteworthy, not only because it improves the previously-known boundaries of intractability for the problem, but also because the underlying reduction allows us to establish - as a simpler case - the NP-hardness of the classical Vertex Disjoint and Edge Disjoint Paths problems with constant path-lengths on grids.

The Computational Complexity of Concise Hypersphere Classification

Hypersphere classification is a classical and foundational method that can provide easy-to-process explanations for the classification of real-valued and binary data. However, obtaining an (ideally concise) explanation via hypersphere classification is much more difficult when dealing with binary data than real-valued data. In this paper, we perform the first complexity-theoretic study of the hypersphere classification problem for binary data. We use the fine-grained parameterized complexity paradigm to analyze the impact of structural properties that may be present in the input data as well as potential conciseness constraints. Our results include stronger lower bounds and new fixed-parameter algorithms for hypersphere classification of binary data, which can find an exact and concise explanation when one exists.

Study on Soft Robotic Pinniped Locomotion

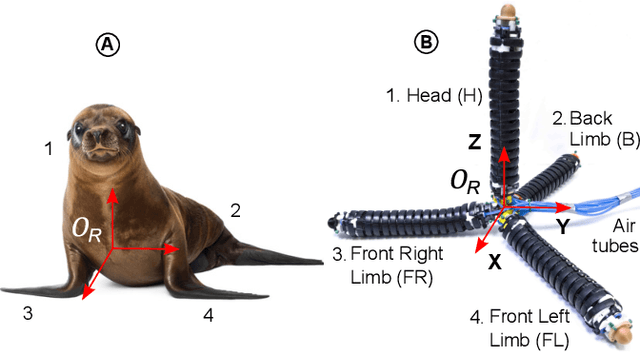
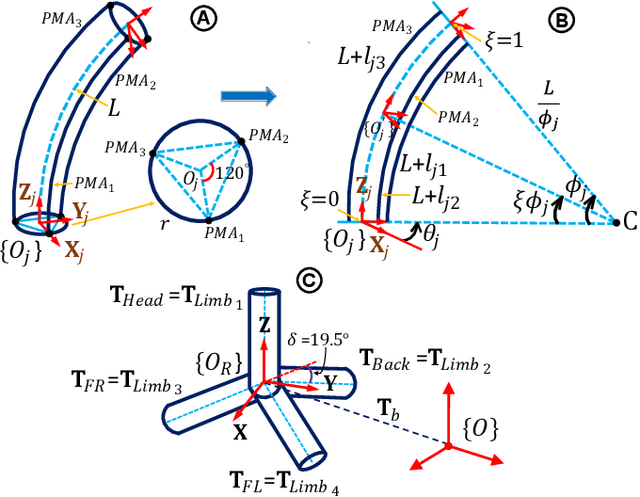
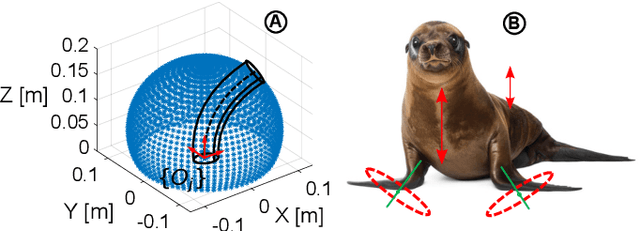
Legged locomotion is a highly promising but under-researched subfield within the field of soft robotics. The compliant limbs of soft-limbed robots offer numerous benefits, including the ability to regulate impacts, tolerate falls, and navigate through tight spaces. These robots have the potential to be used for various applications, such as search and rescue, inspection, surveillance, and more. The state-of-the-art still faces many challenges, including limited degrees of freedom, a lack of diversity in gait trajectories, insufficient limb dexterity, and limited payload capabilities. To address these challenges, we develop a modular soft-limbed robot that can mimic the locomotion of pinnipeds. By using a modular design approach, we aim to create a robot that has improved degrees of freedom, gait trajectory diversity, limb dexterity, and payload capabilities. We derive a complete floating-base kinematic model of the proposed robot and use it to generate and experimentally validate a variety of locomotion gaits. Results show that the proposed robot is capable of replicating these gaits effectively. We compare the locomotion trajectories under different gait parameters against our modeling results to demonstrate the validity of our proposed gait models.

Teleoperation of Soft Modular Robots: Study on Real-time Stability and Gait Control

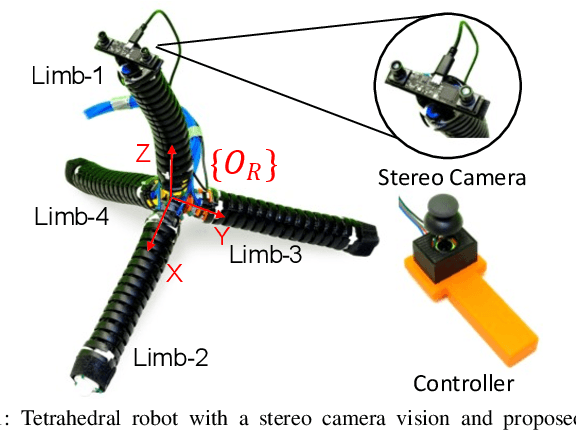
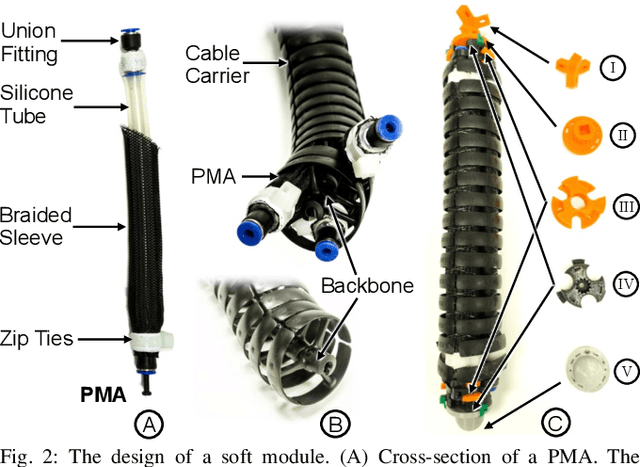
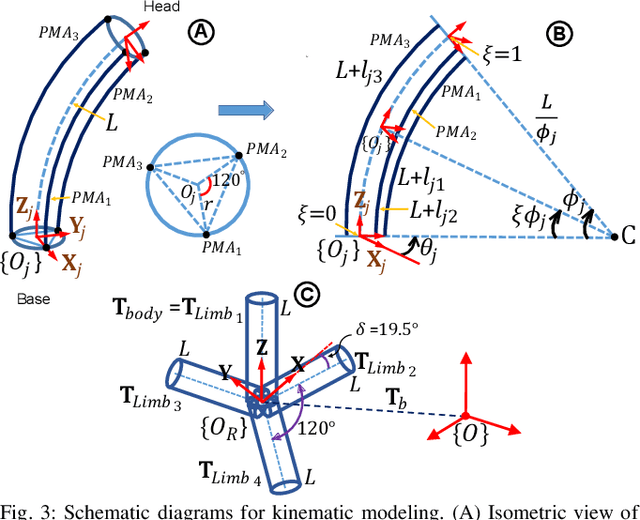
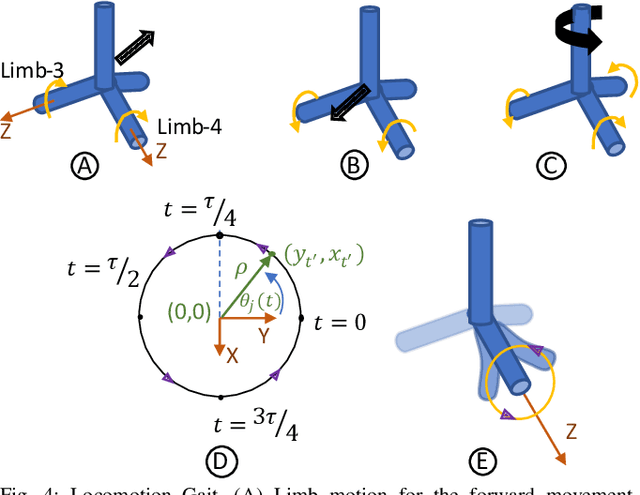
Soft robotics holds tremendous potential for various applications, especially in unstructured environments such as search and rescue operations. However, the lack of autonomy and teleoperability, limited capabilities, absence of gait diversity and real-time control, and onboard sensors to sense the surroundings are some of the common issues with soft-limbed robots. To overcome these limitations, we propose a spatially symmetric, topologically-stable, soft-limbed tetrahedral robot that can perform multiple locomotion gaits. We introduce a kinematic model, derive locomotion trajectories for different gaits, and design a teleoperation mechanism to enable real-time human-robot collaboration. We use the kinematic model to map teleoperation inputs and ensure smooth transitions between gaits. Additionally, we leverage the passive compliance and natural stability of the robot for toppling and obstacle navigation. Through experimental tests, we demonstrate the robot's ability to tackle various locomotion challenges, adapt to different situations, and navigate obstructed environments via teleoperation.

Wheelless Soft Robotic Snake Locomotion: Study on Sidewinding and Helical Rolling Gaits

Soft robotic snakes (SRSs) have a unique combination of continuous and compliant properties that allow them to imitate the complex movements of biological snakes. Despite the previous attempts to develop SRSs, many have been limited to planar movements or use wheels to achieve locomotion, which restricts their ability to imitate the full range of biological snake movements. We propose a new design for the SRSs that is wheelless and powered by pneumatics, relying solely on spatial bending to achieve its movements. We derive a kinematic model of the proposed SRS and utilize it to achieve two snake locomotion trajectories, namely sidewinding and helical rolling. These movements are experimentally evaluated under different gait parameters on our SRS prototype. The results demonstrate that the SRS can successfully mimic the proposed spatial locomotion trajectories. This is a significant improvement over the previous designs, which were either limited to planar movements or relied on wheels for locomotion. The ability of the SRS to effectively mimic the complex movements of biological snakes opens up new possibilities for its use in various applications.

Dynamic Modeling and Validation of Soft Robotic Snake Locomotion

Soft robotic snakes made of compliant materials can continuously deform their bodies and, therefore, mimic the biological snakes' flexible and agile locomotion gaits better than their rigid-bodied counterparts. Without wheel support, to date, soft robotic snakes are limited to emulating planar locomotion gaits, which are derived via kinematic modeling and tested on robotic prototypes. Given that the snake locomotion results from the reaction forces due to the distributed contact between their skin and the ground, it is essential to investigate the locomotion gaits through efficient dynamic models capable of accommodating distributed contact forces. We present a complete spatial dynamic model that utilizes a floating-base kinematic model with distributed contact dynamics for a pneumatically powered soft robotic snake. We numerically evaluate the feasibility of the planar and spatial rolling gaits utilizing the proposed model and experimentally validate the corresponding locomotion gait trajectories on a soft robotic snake prototype. We qualitatively and quantitatively compare the numerical and experimental results which confirm the validity of the proposed dynamic model.

Near-optimal Smooth Path Planning for Multisection Continuum Arms

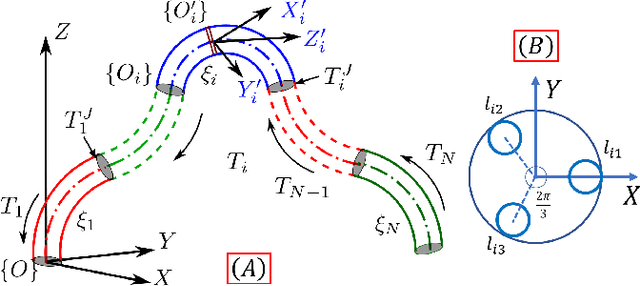
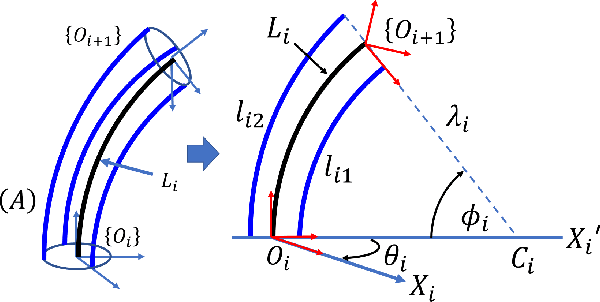
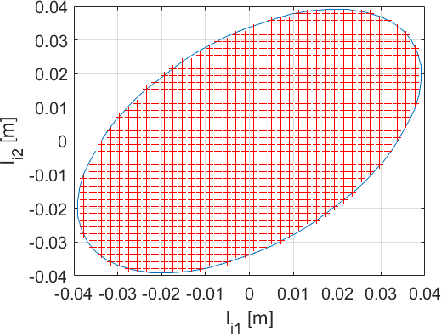
We study the path planning problem for continuum-arm robots, in which we are given a starting and an end point, and we need to compute a path for the tip of the continuum arm between the two points. We consider both cases where obstacles are present and where they are not. We demonstrate how to leverage the continuum arm features to introduce a new model that enables a path planning approach based on the configurations graph, for a continuum arm consisting of three sections, each consisting of three muscle actuators. The algorithm we apply to the configurations graph allows us to exploit parallelism in the computation to obtain efficient implementation. We conducted extensive tests, and the obtained results show the completeness of the proposed algorithm under the considered discretizations, in both cases where obstacles are present and where they are not. We compared our approach to the standard inverse kinematics approach. While the inverse kinematics approach is much faster when successful, our algorithm always succeeds in finding a path or reporting that no path exists, compared to a roughly 70% success rate of the inverse kinematics approach (when a path exists).

Local Backbones

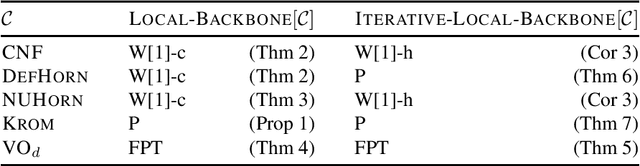
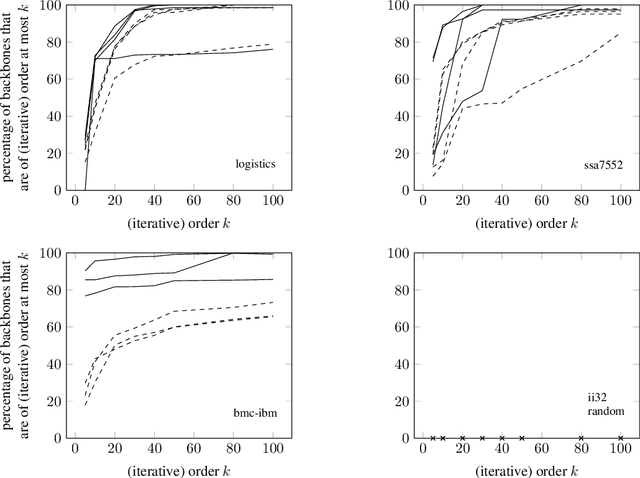
A backbone of a propositional CNF formula is a variable whose truth value is the same in every truth assignment that satisfies the formula. The notion of backbones for CNF formulas has been studied in various contexts. In this paper, we introduce local variants of backbones, and study the computational complexity of detecting them. In particular, we consider k-backbones, which are backbones for sub-formulas consisting of at most k clauses, and iterative k-backbones, which are backbones that result after repeated instantiations of k-backbones. We determine the parameterized complexity of deciding whether a variable is a k-backbone or an iterative k-backbone for various restricted formula classes, including Horn, definite Horn, and Krom. We also present some first empirical results regarding backbones for CNF-Satisfiability (SAT). The empirical results we obtain show that a large fraction of the backbones of structured SAT instances are local, in contrast to random instances, which appear to have few local backbones.