Local Backbones
Paper and Code
Jul 18, 2014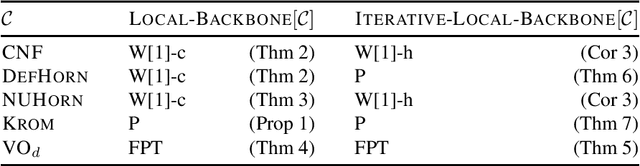
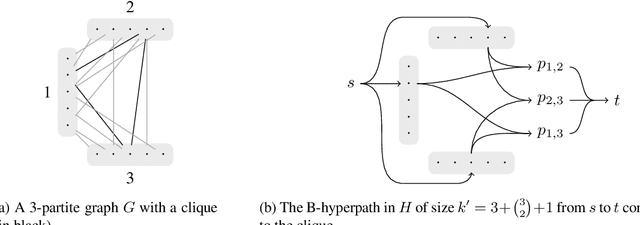
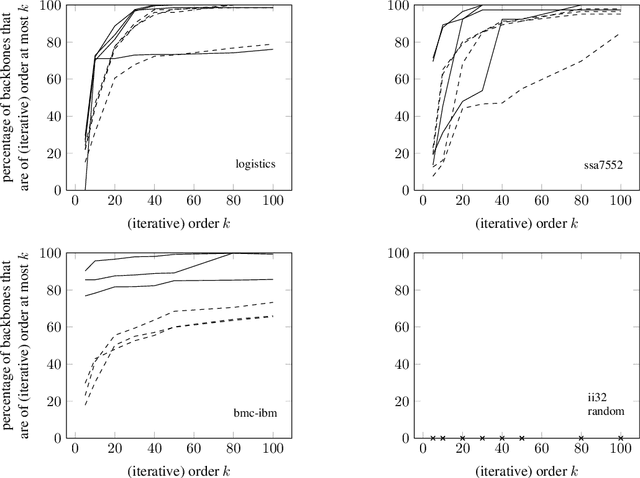
A backbone of a propositional CNF formula is a variable whose truth value is the same in every truth assignment that satisfies the formula. The notion of backbones for CNF formulas has been studied in various contexts. In this paper, we introduce local variants of backbones, and study the computational complexity of detecting them. In particular, we consider k-backbones, which are backbones for sub-formulas consisting of at most k clauses, and iterative k-backbones, which are backbones that result after repeated instantiations of k-backbones. We determine the parameterized complexity of deciding whether a variable is a k-backbone or an iterative k-backbone for various restricted formula classes, including Horn, definite Horn, and Krom. We also present some first empirical results regarding backbones for CNF-Satisfiability (SAT). The empirical results we obtain show that a large fraction of the backbones of structured SAT instances are local, in contrast to random instances, which appear to have few local backbones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge