A Belief Model for Conflicting and Uncertain Evidence -- Connecting Dempster-Shafer Theory and the Topology of Evidence

One problem to solve in the context of information fusion, decision-making, and other artificial intelligence challenges is to compute justified beliefs based on evidence. In real-life examples, this evidence may be inconsistent, incomplete, or uncertain, making the problem of evidence fusion highly non-trivial. In this paper, we propose a new model for measuring degrees of beliefs based on possibly inconsistent, incomplete, and uncertain evidence, by combining tools from Dempster-Shafer Theory and Topological Models of Evidence. Our belief model is more general than the aforementioned approaches in two important ways: (1) it can reproduce them when appropriate constraints are imposed, and, more notably, (2) it is flexible enough to compute beliefs according to various standards that represent agents' evidential demands. The latter novelty allows the users of our model to employ it to compute an agent's (possibly) distinct degrees of belief, based on the same evidence, in situations when, e.g, the agent prioritizes avoiding false negatives and when it prioritizes avoiding false positives. Finally, we show that computing degrees of belief with this model is #P-complete in general.

Egalitarian Judgment Aggregation

Egalitarian considerations play a central role in many areas of social choice theory. Applications of egalitarian principles range from ensuring everyone gets an equal share of a cake when deciding how to divide it, to guaranteeing balance with respect to gender or ethnicity in committee elections. Yet, the egalitarian approach has received little attention in judgment aggregation -- a powerful framework for aggregating logically interconnected issues. We make the first steps towards filling that gap. We introduce axioms capturing two classical interpretations of egalitarianism in judgment aggregation and situate these within the context of existing axioms in the pertinent framework of belief merging. We then explore the relationship between these axioms and several notions of strategyproofness from social choice theory at large. Finally, a novel egalitarian judgment aggregation rule stems from our analysis; we present complexity results concerning both outcome determination and strategic manipulation for that rule.

A Parameterized Complexity View on Description Logic Reasoning

Description logics are knowledge representation languages that have been designed to strike a balance between expressivity and computational tractability. Many different description logics have been developed, and numerous computational problems for these logics have been studied for their computational complexity. However, essentially all complexity analyses of reasoning problems for description logics use the one-dimensional framework of classical complexity theory. The multi-dimensional framework of parameterized complexity theory is able to provide a much more detailed image of the complexity of reasoning problems. In this paper we argue that the framework of parameterized complexity has a lot to offer for the complexity analysis of description logic reasoning problems---when one takes a progressive and forward-looking view on parameterized complexity tools. We substantiate our argument by means of three case studies. The first case study is about the problem of concept satisfiability for the logic ALC with respect to nearly acyclic TBoxes. The second case study concerns concept satisfiability for ALC concepts parameterized by the number of occurrences of union operators and the number of occurrences of full existential quantification. The third case study offers a critical look at data complexity results from a parameterized complexity point of view. These three case studies are representative for the wide range of uses for parameterized complexity methods for description logic problems.

Hunting for Tractable Languages for Judgment Aggregation

Judgment aggregation is a general framework for collective decision making that can be used to model many different settings. Due to its general nature, the worst case complexity of essentially all relevant problems in this framework is very high. However, these intractability results are mainly due to the fact that the language to represent the aggregation domain is overly expressive. We initiate an investigation of representation languages for judgment aggregation that strike a balance between (1) being limited enough to yield computational tractability results and (2) being expressive enough to model relevant applications. In particular, we consider the languages of Krom formulas, (definite) Horn formulas, and Boolean circuits in decomposable negation normal form (DNNF). We illustrate the use of the positive complexity results that we obtain for these languages with a concrete application: voting on how to spend a budget (i.e., participatory budgeting).

Expressing Linear Orders Requires Exponential-Size DNNFs

We show that any DNNF circuit that expresses the set of linear orders over a set of $n$ candidates must be of size $2^{\Omega(n)}$. Moreover, we show that there exist DNNF circuits of size $2^{O(n)}$ expressing linear orders over $n$ candidates.

On the Computational Complexity of Model Checking for Dynamic Epistemic Logic with S5 Models

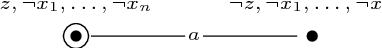
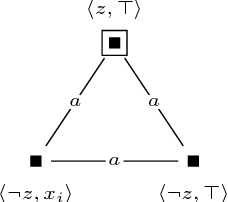
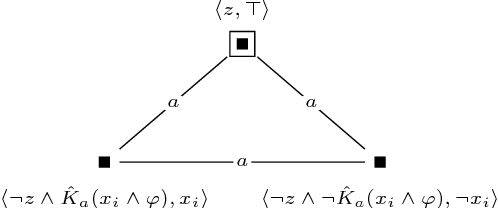
Dynamic epistemic logic (DEL) is a logical framework for representing and reasoning about knowledge change for multiple agents. An important computational task in this framework is the model checking problem, which has been shown to be PSPACE-hard even for S5 models and two agents. We answer open questions in the literature about the complexity of this problem in more restricted settings. We provide a detailed complexity analysis of the model checking problem for DEL, where we consider various combinations of restrictions, such as the number of agents, whether the models are single-pointed or multi-pointed, and whether postconditions are allowed in the updates. In particular, we show that the problem is already PSPACE-hard in (1) the case of one agent, multi-pointed S5 models, and no postconditions, and (2) the case of two agents, only single-pointed S5 models, and no postconditions. In addition, we study the setting where only semi-private announcements are allowed as updates. We show that for this case the problem is already PSPACE-hard when restricted to two agents and three propositional variables.

Complexity Results for Manipulation, Bribery and Control of the Kemeny Procedure in Judgment Aggregation

We study the computational complexity of several scenarios of strategic behavior for the Kemeny procedure in the setting of judgment aggregation. In particular, we investigate (1) manipulation, where an individual aims to achieve a better group outcome by reporting an insincere individual opinion, (2) bribery, where an external agent aims to achieve an outcome with certain properties by bribing a number of individuals, and (3) control (by adding or deleting issues), where an external agent aims to achieve an outcome with certain properties by influencing the set of issues in the judgment aggregation situation. We show that determining whether these types of strategic behavior are possible (and if so, computing a policy for successful strategic behavior) is complete for the second level of the Polynomial Hierarchy. That is, we show that these problems are $\Sigma^p_2$-complete.

Local Backbones

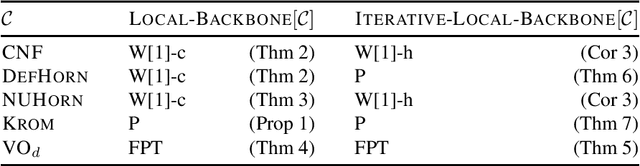
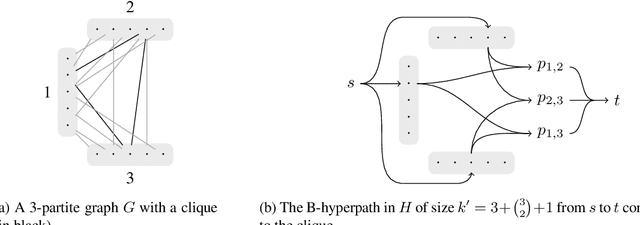
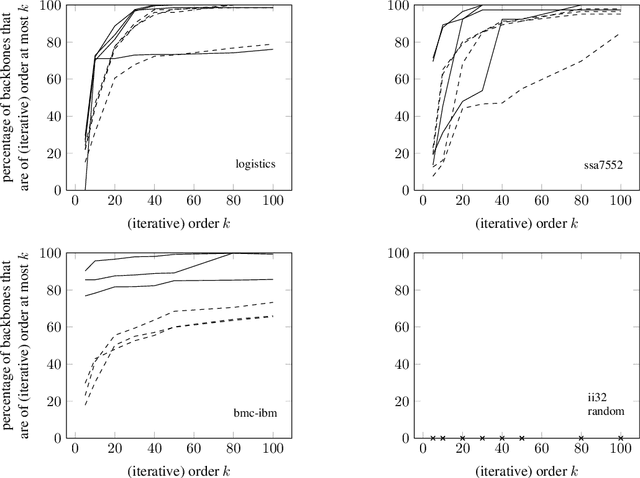
A backbone of a propositional CNF formula is a variable whose truth value is the same in every truth assignment that satisfies the formula. The notion of backbones for CNF formulas has been studied in various contexts. In this paper, we introduce local variants of backbones, and study the computational complexity of detecting them. In particular, we consider k-backbones, which are backbones for sub-formulas consisting of at most k clauses, and iterative k-backbones, which are backbones that result after repeated instantiations of k-backbones. We determine the parameterized complexity of deciding whether a variable is a k-backbone or an iterative k-backbone for various restricted formula classes, including Horn, definite Horn, and Krom. We also present some first empirical results regarding backbones for CNF-Satisfiability (SAT). The empirical results we obtain show that a large fraction of the backbones of structured SAT instances are local, in contrast to random instances, which appear to have few local backbones.

Parameterized Complexity Results for Plan Reuse

Planning is a notoriously difficult computational problem of high worst-case complexity. Researchers have been investing significant efforts to develop heuristics or restrictions to make planning practically feasible. Case-based planning is a heuristic approach where one tries to reuse previous experience when solving similar problems in order to avoid some of the planning effort. Plan reuse may offer an interesting alternative to plan generation in some settings. We provide theoretical results that identify situations in which plan reuse is provably tractable. We perform our analysis in the framework of parameterized complexity, which supports a rigorous worst-case complexity analysis that takes structural properties of the input into account in terms of parameters. A central notion of parameterized complexity is fixed-parameter tractability which extends the classical notion of polynomial-time tractability by utilizing the effect of structural properties of the problem input. We draw a detailed map of the parameterized complexity landscape of several variants of problems that arise in the context of case-based planning. In particular, we consider the problem of reusing an existing plan, imposing various restrictions in terms of parameters, such as the number of steps that can be added to the existing plan to turn it into a solution of the planning instance at hand.

The RegularGcc Matrix Constraint

We study propagation of the RegularGcc global constraint. This ensures that each row of a matrix of decision variables satisfies a Regular constraint, and each column satisfies a Gcc constraint. On the negative side, we prove that propagation is NP-hard even under some strong restrictions (e.g. just 3 values, just 4 states in the automaton, or just 5 columns to the matrix). On the positive side, we identify two cases where propagation is fixed parameter tractable. In addition, we show how to improve propagation over a simple decomposition into separate Regular and Gcc constraints by identifying some necessary but insufficient conditions for a solution. We enforce these conditions with some additional weighted row automata. Experimental results demonstrate the potential of these methods on some standard benchmark problems.