Structural perspective on constraint-based learning of Markov networks

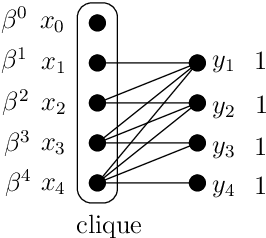
Markov networks are probabilistic graphical models that employ undirected graphs to depict conditional independence relationships among variables. Our focus lies in constraint-based structure learning, which entails learning the undirected graph from data through the execution of conditional independence tests. We establish theoretical limits concerning two critical aspects of constraint-based learning of Markov networks: the number of tests and the sizes of the conditioning sets. These bounds uncover an exciting interplay between the structural properties of the graph and the amount of tests required to learn a Markov network. The starting point of our work is that the graph parameter maximum pairwise connectivity, $\kappa$, that is, the maximum number of vertex-disjoint paths connecting a pair of vertices in the graph, is responsible for the sizes of independence tests required to learn the graph. On one hand, we show that at least one test with the size of the conditioning set at least $\kappa$ is always necessary. On the other hand, we prove that any graph can be learned by performing tests of size at most $\kappa$. This completely resolves the question of the minimum size of conditioning sets required to learn the graph. When it comes to the number of tests, our upper bound on the sizes of conditioning sets implies that every $n$-vertex graph can be learned by at most $n^{\kappa}$ tests with conditioning sets of sizes at most $\kappa$. We show that for any upper bound $q$ on the sizes of the conditioning sets, there exist graphs with $O(n q)$ vertices that require at least $n^{\Omega(\kappa)}$ tests to learn. This lower bound holds even when the treewidth and the maximum degree of the graph are at most $\kappa+2$. On the positive side, we prove that every graph of bounded treewidth can be learned by a polynomial number of tests with conditioning sets of sizes at most $2\kappa$.

How to Find a Good Explanation for Clustering?

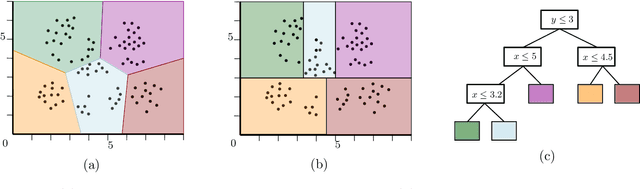
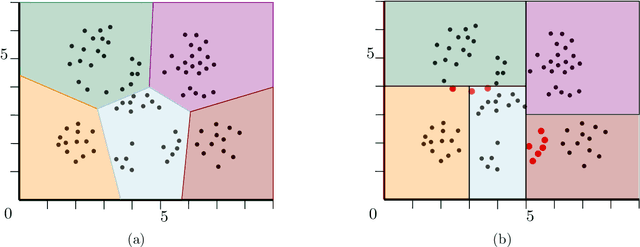
$k$-means and $k$-median clustering are powerful unsupervised machine learning techniques. However, due to complicated dependences on all the features, it is challenging to interpret the resulting cluster assignments. Moshkovitz, Dasgupta, Rashtchian, and Frost [ICML 2020] proposed an elegant model of explainable $k$-means and $k$-median clustering. In this model, a decision tree with $k$ leaves provides a straightforward characterization of the data set into clusters. We study two natural algorithmic questions about explainable clustering. (1) For a given clustering, how to find the "best explanation" by using a decision tree with $k$ leaves? (2) For a given set of points, how to find a decision tree with $k$ leaves minimizing the $k$-means/median objective of the resulting explainable clustering? To address the first question, we introduce a new model of explainable clustering. Our model, inspired by the notion of outliers in robust statistics, is the following. We are seeking a small number of points (outliers) whose removal makes the existing clustering well-explainable. For addressing the second question, we initiate the study of the model of Moshkovitz et al. from the perspective of multivariate complexity. Our rigorous algorithmic analysis sheds some light on the influence of parameters like the input size, dimension of the data, the number of outliers, the number of clusters, and the approximation ratio, on the computational complexity of explainable clustering.

Present-Biased Optimization

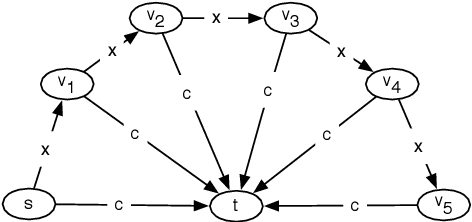
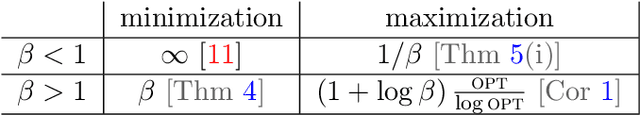
This paper explores the behavior of present-biased agents, that is, agents who erroneously anticipate the costs of future actions compared to their real costs. Specifically, the paper extends the original framework proposed by Akerlof (1991) for studying various aspects of human behavior related to time-inconsistent planning, including procrastination, and abandonment, as well as the elegant graph-theoretic model encapsulating this framework recently proposed by Kleinberg and Oren (2014). The benefit of this extension is twofold. First, it enables to perform fine grained analysis of the behavior of present-biased agents depending on the optimisation task they have to perform. In particular, we study covering tasks vs. hitting tasks, and show that the ratio between the cost of the solutions computed by present-biased agents and the cost of the optimal solutions may differ significantly depending on the problem constraints. Second, our extension enables to study not only underestimation of future costs, coupled with minimization problems, but also all combinations of minimization/maximization, and underestimation/overestimation. We study the four scenarios, and we establish upper bounds on the cost ratio for three of them (the cost ratio for the original scenario was known to be unbounded), providing a complete global picture of the behavior of present-biased agents, as far as optimisation tasks are concerned.

EPTAS for $k$-means Clustering of Affine Subspaces

We consider a generalization of the fundamental $k$-means clustering for data with incomplete or corrupted entries. When data objects are represented by points in $\mathbb{R}^d$, a data point is said to be incomplete when some of its entries are missing or unspecified. An incomplete data point with at most $\Delta$ unspecified entries corresponds to an axis-parallel affine subspace of dimension at most $\Delta$, called a $\Delta$-point. Thus we seek a partition of $n$ input $\Delta$-points into $k$ clusters minimizing the $k$-means objective. For $\Delta=0$, when all coordinates of each point are specified, this is the usual $k$-means clustering. We give an algorithm that finds an $(1+ \epsilon)$-approximate solution in time $f(k,\epsilon, \Delta) \cdot n^2 \cdot d$ for some function $f$ of $k,\epsilon$, and $\Delta$ only.

On Coresets for Fair Clustering in Metric and Euclidean Spaces and Their Applications

Fair clustering is a constrained variant of clustering where the goal is to partition a set of colored points, such that the fraction of points of any color in every cluster is more or less equal to the fraction of points of this color in the dataset. This variant was recently introduced by Chierichetti et al. [NeurIPS, 2017] in a seminal work and became widely popular in the clustering literature. In this paper, we propose a new construction of coresets for fair clustering based on random sampling. The new construction allows us to obtain the first coreset for fair clustering in general metric spaces. For Euclidean spaces, we obtain the first coreset whose size does not depend exponentially on the dimension. Our coreset results solve open questions proposed by Schmidt et al. [WAOA, 2019] and Huang et al. [NeurIPS, 2019]. The new coreset construction helps to design several new approximation and streaming algorithms. In particular, we obtain the first true constant-approximation algorithm for metric fair clustering, whose running time is fixed-parameter tractable (FPT). In the Euclidean case, we derive the first $(1+\epsilon)$-approximation algorithm for fair clustering whose time complexity is near-linear and does not depend exponentially on the dimension of the space. Besides, our coreset construction scheme is fairly general and gives rise to coresets for a wide range of constrained clustering problems. This leads to improved constant-approximations for these problems in general metrics and near-linear time $(1+\epsilon)$-approximations in the Euclidean metric.

Refined Complexity of PCA with Outliers

Principal component analysis (PCA) is one of the most fundamental procedures in exploratory data analysis and is the basic step in applications ranging from quantitative finance and bioinformatics to image analysis and neuroscience. However, it is well-documented that the applicability of PCA in many real scenarios could be constrained by an "immune deficiency" to outliers such as corrupted observations. We consider the following algorithmic question about the PCA with outliers. For a set of $n$ points in $\mathbb{R}^{d}$, how to learn a subset of points, say 1% of the total number of points, such that the remaining part of the points is best fit into some unknown $r$-dimensional subspace? We provide a rigorous algorithmic analysis of the problem. We show that the problem is solvable in time $n^{O(d^2)}$. In particular, for constant dimension the problem is solvable in polynomial time. We complement the algorithmic result by the lower bound, showing that unless Exponential Time Hypothesis fails, in time $f(d)n^{o(d)}$, for any function $f$ of $d$, it is impossible not only to solve the problem exactly but even to approximate it within a constant factor.

Approximation Schemes for Low-Rank Binary Matrix Approximation Problems

We provide a randomized linear time approximation scheme for a generic problem about clustering of binary vectors subject to additional constrains. The new constrained clustering problem encompasses a number of problems and by solving it, we obtain the first linear time-approximation schemes for a number of well-studied fundamental problems concerning clustering of binary vectors and low-rank approximation of binary matrices. Among the problems solvable by our approach are \textsc{Low GF(2)-Rank Approximation}, \textsc{Low Boolean-Rank Approximation}, and various versions of \textsc{Binary Clustering}. For example, for \textsc{Low GF(2)-Rank Approximation} problem, where for an $m\times n$ binary matrix $A$ and integer $r>0$, we seek for a binary matrix $B$ of $GF_2$ rank at most $r$ such that $\ell_0$ norm of matrix $A-B$ is minimum, our algorithm, for any $\epsilon>0$ in time $ f(r,\epsilon)\cdot n\cdot m$, where $f$ is some computable function, outputs a $(1+\epsilon)$-approximate solution with probability at least $(1-\frac{1}{e})$. Our approximation algorithms substantially improve the running times and approximation factors of previous works. We also give (deterministic) PTASes for these problems running in time $n^{f(r)\frac{1}{\epsilon^2}\log \frac{1}{\epsilon}}$, where $f$ is some function depending on the problem. Our algorithm for the constrained clustering problem is based on a novel sampling lemma, which is interesting in its own.