Present-Biased Optimization

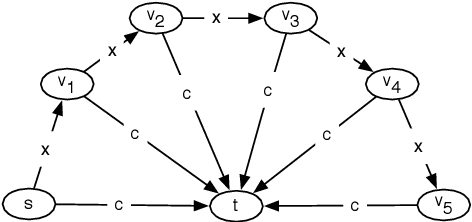
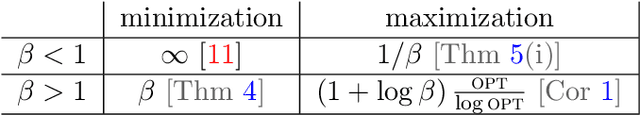
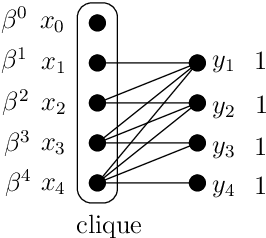
This paper explores the behavior of present-biased agents, that is, agents who erroneously anticipate the costs of future actions compared to their real costs. Specifically, the paper extends the original framework proposed by Akerlof (1991) for studying various aspects of human behavior related to time-inconsistent planning, including procrastination, and abandonment, as well as the elegant graph-theoretic model encapsulating this framework recently proposed by Kleinberg and Oren (2014). The benefit of this extension is twofold. First, it enables to perform fine grained analysis of the behavior of present-biased agents depending on the optimisation task they have to perform. In particular, we study covering tasks vs. hitting tasks, and show that the ratio between the cost of the solutions computed by present-biased agents and the cost of the optimal solutions may differ significantly depending on the problem constraints. Second, our extension enables to study not only underestimation of future costs, coupled with minimization problems, but also all combinations of minimization/maximization, and underestimation/overestimation. We study the four scenarios, and we establish upper bounds on the cost ratio for three of them (the cost ratio for the original scenario was known to be unbounded), providing a complete global picture of the behavior of present-biased agents, as far as optimisation tasks are concerned.

Delays Induce an Exponential Memory Gap for Rendezvous in Trees

The aim of rendezvous in a graph is meeting of two mobile agents at some node of an unknown anonymous connected graph. In this paper, we focus on rendezvous in trees, and, analogously to the efforts that have been made for solving the exploration problem with compact automata, we study the size of memory of mobile agents that permits to solve the rendezvous problem deterministically. We assume that the agents are identical, and move in synchronous rounds. We first show that if the delay between the starting times of the agents is arbitrary, then the lower bound on memory required for rendezvous is Omega(log n) bits, even for the line of length n. This lower bound meets a previously known upper bound of O(log n) bits for rendezvous in arbitrary graphs of size at most n. Our main result is a proof that the amount of memory needed for rendezvous with simultaneous start depends essentially on the number L of leaves of the tree, and is exponentially less impacted by the number n of nodes. Indeed, we present two identical agents with O(log L + loglog n) bits of memory that solve the rendezvous problem in all trees with at most n nodes and at most L leaves. Hence, for the class of trees with polylogarithmically many leaves, there is an exponential gap in minimum memory size needed for rendezvous between the scenario with arbitrary delay and the scenario with delay zero. Moreover, we show that our upper bound is optimal by proving that Omega(log L + loglog n)$ bits of memory are required for rendezvous, even in the class of trees with degrees bounded by 3.